EDP et Lax-Milgram (coercivité)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lakers21
- Messages: 7
- Enregistré le: 25 Mai 2008, 12:38
-
 par lakers21 » 29 Déc 2014, 10:17
par lakers21 » 29 Déc 2014, 10:17
Bonjour,
Je souhaiterais montrer proprement le caractère elliptique/coercive de la forme bilinéaire

afin d'appliquer le théorème de Lax-Milgram :
, a(u,u) \geq C ||u||_{H^{1}(\omega)}^2)
où
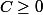
)
est l'espace considéré ici.
 = \int_{\omega}{\nabla{u}\nabla{v}} + (\int_{\omega}{u}) (\int_{\omega}{v}))
Comment minorer alors
 = \int_{\omega}{\nabla{u}^2} + (\int_{\omega}{u})^2)
par
}^2 = \int_{\omega}{|\nabla{u}|^2} + \int_{\omega}{|u|^2})
Merci d'avance!
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 29 Déc 2014, 12:25
par Luc » 29 Déc 2014, 12:25
lakers21 a écrit:Bonjour,
Je souhaiterais montrer proprement le caractère elliptique/coercive de la forme bilinéaire

afin d'appliquer le théorème de Lax-Milgram :
, a(u,u) \geq C ||u||_{H^{1}(\omega)}^2)
où
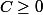
)
est l'espace considéré ici.
 = \int_{\omega}{\nabla{u}\nabla{v}} + (\int_{\omega}{u}) (\int_{\omega}{v}))
Comment minorer alors
 = \int_{\omega}{\nabla{u}^2} + (\int_{\omega}{u})^2)
par
}^2 = \int_{\omega}{|\nabla{u}|^2} + \int_{\omega}{|u|^2})
Merci d'avance!
Bonjour,
Cauchy-Schwarz, non?
Luc
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités