EDO second ordre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zaytoun
- Messages: 5
- Enregistré le: 25 Déc 2007, 17:34
-
 par zaytoun » 25 Déc 2007, 17:39
par zaytoun » 25 Déc 2007, 17:39
Bonjour,
Je cherche désespérement une solution particulière de l'EDO suivante :
 + xf(x) = 0)
Auriez-vous une idée ?
Merci d'avance.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 25 Déc 2007, 18:06
par Flodelarab » 25 Déc 2007, 18:06
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 25 Déc 2007, 18:07
par cesar » 25 Déc 2007, 18:07
as tu essayé une solution sous forme de serie entiere ? (somme de a(n).X^n, n variant de 0 à + l'infini), avec le produit xf(x), cela devrait s'arranger au poil...si la solution f(x)=0 ne te satisfait pas...
j'arrive à une relation de la forme (n+2)(n+1) a(n+2) + a(n-1) = 0 pour X^n
n variant de 1 à l'infini. sans garantie : j'ai fait ça sur le pouce...
-
zaytoun
- Messages: 5
- Enregistré le: 25 Déc 2007, 17:34
-
 par zaytoun » 25 Déc 2007, 18:15
par zaytoun » 25 Déc 2007, 18:15
Moi je trouve (n+3)(n+2)a_{n+3} + a_n = 0
Oups je n'ai rien dit
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 25 Déc 2007, 18:18
par cesar » 25 Déc 2007, 18:18
zaytoun a écrit:Moi je trouve (n+3)(n+2)a_{n+3} + a_n = 0
Oups je n'ai rien dit
cela me rassure : c'est la meme chose, mais avec un n different...
-
zaytoun
- Messages: 5
- Enregistré le: 25 Déc 2007, 17:34
-
 par zaytoun » 25 Déc 2007, 18:19
par zaytoun » 25 Déc 2007, 18:19
Je trouve :
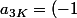^k\frac{a_0}{3k!}\prod_{p=0}^{k-1}(1+3p))
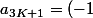^k\frac{a_1}{(3k+1)!}\prod_{p=0}^{k-1}(2+3p))

Mais comment calculer le rayon de convergence, je ne peux pas utiliser d'Alembert ici ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 25 Déc 2007, 18:33
par leon1789 » 25 Déc 2007, 18:33
zaytoun a écrit:Bonjour,
Je cherche désespérement une solution particulière de l'EDO suivante :
 + xf(x) = 0)
Auriez-vous une idée ?
Merci d'avance.
C'est une équation homogène, ie. avec un second membre nul (à droite de l'égalité). Dans ce cas, il y a une solution particulière triviale, comme l'a signalé Flodelarab. D'ailleurs, on n'en parle jamais (puisque sans intérêt).
Ce qui me titille, c'est pourquoi tu poses la question... As-tu compris ?
-
zaytoun
- Messages: 5
- Enregistré le: 25 Déc 2007, 17:34
-
 par zaytoun » 25 Déc 2007, 18:44
par zaytoun » 25 Déc 2007, 18:44
Initialement, je cherchais une solution particulière pour, en utilisant le Wronskien, en déduire toutes les solutions.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 25 Déc 2007, 19:06
par leon1789 » 25 Déc 2007, 19:06
zaytoun a écrit:Initialement, je cherchais une solution particulière pour, en utilisant le Wronskien, en déduire toutes les solutions.
Mais ta solution particulière doit vérifier quelque chose de particulier ?
-
zaytoun
- Messages: 5
- Enregistré le: 25 Déc 2007, 17:34
-
 par zaytoun » 25 Déc 2007, 19:23
par zaytoun » 25 Déc 2007, 19:23
leon1789 a écrit:Mais ta solution particulière doit vérifier quelque chose de particulier ?
Non, aucune condition supplémentaire.
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 26 Déc 2007, 08:24
par cesar » 26 Déc 2007, 08:24
zaytoun a écrit:Je trouve :
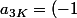^k\frac{a_0}{3k!}\prod_{p=0}^{k-1}(1+3p))
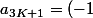^k\frac{a_1}{(3k+1)!}\prod_{p=0}^{k-1}(2+3p))

Mais comment calculer le rayon de convergence, je ne peux pas utiliser d'Alembert ici ?
tu as desormais deux solutions independantes de ton equation (elles n'ont pas de terme en x^n en commun)
et elles sont de la forme :
f1(x) = H(x^3)
et
f2(x) = x.G(x^3)
reste à voir ce que cela donne dans l'équa diff...
additif : je l'ai fait, et je suis tombé sur des équations de riccati....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités