Edo

[barbu23]

Bonjour à tous : :happy3:
Quelqu'un peut -t-il m'aider à resoudre l'équation differentielle suivante :

avec : .
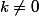
Merci d'avance. :happy3:

[Black Jack]

y' = k.y³

y = 0 est solution.
si y est différent de 0, on peut écrire :

y'/y³ = k

et on intégrant les 2 membres ...

:zen:

[barbu23]

Oui , c'est vrai tu as raison , c'est très simple ! :happy3:
Merci beaucoup. :happy3:

[alavacommejetepousse]

y' = k.y³

y = 0 est solution.
si y est différent de 0, on peut écrire :

y'/y³ = k

et on intégrant les 2 membres ...

:zen:

bonjour je dirais plutôt si y ne s annule pas

[charif]

bs


certains matheux sont alérgiques à cette façon de résoudre une équation diff

c'est plutôt réservé à la physique car la plus part des solutions vérifiées les hypothèses

conseil : n'utilisez jamais cette méthode en mathématiques

[Black Jack]

bs


certains matheux sont alérgiques à cette façon de résoudre une équation diff

c'est plutôt réservé à la physique car la plus part des solutions vérifiées les hypothèses

conseil : n'utilisez jamais cette méthode en mathématiques

Il ne faut pas croire ce que certains affirment sur la soit-disant non rigueur mathématique du procédé dont tu parles ici (mais il doit être utilisé avec certaines précautions ...)

La lecture de ce lien est à recommander :

http://www.scribd.com/doc/14755203/Une-querelle-des-Anciens-et-des-Modernes

Il devrait permettre de remettre certains a priori largement répandus à leur place.

:zen:

[charif]

bs

alors écrivez ce lien dans une copie d'examen ou un concours pour convaincre le correcteur

il faut soigné votre façon de rédiger sinon vous aurez tjrs la moitié de la note

[Black Jack]

bs

alors écrivez ce lien dans une copie d'examen ou un concours pour convaincre le correcteur

il faut soigné votre façon de rédiger sinon vous aurez tjrs la moitié de la note

Mon but n'est pas d'essayer de convaincre un correcteur mais de faire des résolutions correctes, c'est fondamentalement différent.

Remarque, que si tu n'apprécies pas le lien donné (au contraire de moi), on peut renvoyer sur des liens concernant la résolution d'équations différentielles à variables séparables et pour les courageux à des liens vers la théorie de "l'Analyse non Standard" mais cette dernière n'est pas accessible dans les études niveaux secondaires.


:zen:

[charif]

bs

essayez d'améliorer d'abord votre rédaction , et laissez les "non standards" tranquilles vous êtes incapable de donner une rédaction correcte et vous allez à un niveau supérieur ,, c'est grave

[Black Jack]

bs

essayez d'améliorer d'abord votre rédaction , et laissez les "non standards" tranquilles vous êtes incapable de donner une rédaction correcte et vous allez à un niveau supérieur ,, c'est grave

Le but n'est pas de faire le problème à la place de celui qui pose la question et donc surtout pas de lui macher toute la rédaction, juste une indication dans une direction possible.

Quand à mon niveau, ne t'en inquiète pas, il est bien suffisant que pour avoir de bonnes notions de l'ANS. (moins que celles de BEN qui est un pro dans le domaine).

Mais même sans rien y connaître en ANS on peut parfaitement traiter le problème avec la technique indiquée pour les équations à variables séparables...
Si elle a été enseignée, ce qui dépend du niveau d'étude et du programme du pays concerné.

Toute autre méthode qui conduit correctement à la résolution est évidemment aussi acceptable.


:zen:

[charif]

bs

pardonez mois monsieur

[kazeriahm]

bah pour le coup c'est très rigoureux

comme déjà dit : y=0 est solution
si y n'est pas identiquement nulle, la partie unicité de Cauchy-Lispchitz nous dit qu'y ne s'annule pas et on peut intégrer l'égalité y'/y^3=k