Ecart-type

[Pseuda]

Bonsoir,

Je me pose une question en probabilités-statistiques concernant l'écart-type, pas facile à exprimer, je vais essayer.

Autant la notion d'espérance mathématique d'une variable aléatoire en probabilité, ou de moyenne en statistiques, me paraît claire, elle correspond à une réalité tangible, autant la notion d'écart-type me paraît plus incertaine, sachant qu'on calcule des carrés d'écarts à la moyenne, dont on prend la racine carrée.
On aurait pu choisir comme mesure de dispersion, l'écart interquartile, la moyenne des valeurs absolues des écarts, etc...

La question est : est-ce que l'écart-type est une donnée fondamentale, ou bien arbitraire ?

Je m'explique : si on réduisait les lois (par exemple les lois binomiales, ...) avec une autre mesure de dispersion, est-ce que les lois centrées réduites convergeraient vers la loi normale centrée réduite (avec sa fonction de densité telle qu'on la connaît) ? vers une autre loi continue ? en cloche, ou à peu près ? ne convergeraient vers aucune loi ?

Il me semble que pour répondre à cette question, il faudrait connaître comment fonctionne le TCL (mais peut-être pas).

Merci d'avance à ceux qui voudront bien se pencher sur cette question.

[J0ke]

Hello,

Il y avait en fait deux points de vue, celui de Laplace et celui de Gauss.

Pour une série de données (x1, x2, ..., xn) ils souhaitaient minimiser la valeur de :

pour Gauss et pour Laplace.

Le minimum de G est atteint en la moyenne (l'espérance), celui de L est atteint en la médiane.

Voilà ce que j'en sais.

[zygomatique]

salut

je pense que l'écart type est simplement la racine carrée du moment centré d'ordre 2 (quand il existe) .... qui a le bon gout d'être positif ....

[Pseuda]

Bonjour,

@J0ke
Merci pour cette approche, qui tend à dire que l'écart-type ne joue pas un rôle privilégié en proba-stats, par rapport à d'autres mesures de dispersion. Tout dépend de ce qu'on cherche. Je ne connaissais pas cette propriété de la médiane. Dans ce cas, la moyenne des valeurs absolues des écarts à la médiane fait une mesure de dispersion plus parlante que l'écart-type.

@zygomatique
Mais les autres mesures de dispersion sont aussi positives.

Quand on regarde de près le théorème de Moivre-Laplace (convergence d'une loi binomiale vers la loi normale de même espérance et même écart-type, en centrées réduites), on se rend compte que tout le théorème réside dans la propriété que :

Si X suit la loi binomiale B(n,p), alors P(X=np) (soit la moyenne) 1/ *1/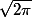, d'autant plus proche que n est grand, avec =écart-type de la loi binomiale.

De même, la probabilité P(X=k), 0kn, est proche d'une valeur qui s'écrit avec l'écart-type de la loi binomiale (longue à écrire ici en Tex), d'autant plus proche que n est grand.

Ceci ferait dire que l'écart-type joue un rôle privilégié par rapport à d'autres mesures de dispersion ? En tout cas, pour la loi des grands nombres (qui est quand même la base sur laquelle se fonde le calcul des probabilités). Mais pas pour d'autres aspects ... Pouvez-vous confirmer ceci ?

Dans tous les cas, j'ai l'impression que cette question se pose confusément dans beaucoup d'esprits, mais que l'emploi de l'écart-type reste difficile à justifier simplement.... Là est le problème.....

[zygomatique]

un moment d'ordre impair peut être négatif ...

une remarque : np n'est pas toujours entier (d'ailleurs la probabilité de choisir un couple (n, p) dans N x [0, 1] tel que np soit entier est nulle .... ce me semble-t-il ....)

une propriété de l'écart type : si f est la densité de probabilité de la loi N(m, s) alors les points d'inflexion de f on pour abscisse m - s et m + s (par symétrie bien sur) ....

[Pseuda]

Je voulais dire : les autres dispersions (écart interquartiles...) aussi sont positives.

Bien entendu, cette formule pour P(X=np) s'applique quand np est un entier (par exemple, n=30 , p=0,4). Je la trouve très étonnante.

En fait, tout simplement, P(X=k) valeur de la fonction de densité de la loi normale de même espérance et même écart-type au point k, soit : (démontré par le théorème de M-L).

Si on prenait pour mesure de dispersion un ', la formule serait , j'imagine, toute différente, c'est-à-dire qu'elle ne consisterait pas juste à remplacer par ' ? Donc l'écart-type joue un rôle privilégié pour la loi des grands nombres ?

Oui les points d'inflexion de la fonction de densité de la loi normale (vers laquelle tend la loi binomiale) se situent à - et + de la moyenne. Autre rôle privilégié ?

[Doraki]

Bien entendu, cette formule pour P(X=np) s'applique quand np est un entier (par exemple, n=30 , p=0,4). Je la trouve très étonnante.

d'où tu sors ça ??
P(X=np) devrait tendre vers 0 quand n tend vers l'infini (en O(1/sqrt(n)) si je me gourre pas ?)

Si tu remplaçes l'écart type par un autre truc dans l'énoncé du théorème centrale limite, tu obtiens un théorème faux, donc ça veut bien dire que l'écart type est important en général.

[Pseuda]

Bien entendu, cette formule pour P(X=np) s'applique quand np est un entier (par exemple, n=30 , p=0,4). Je la trouve très étonnante.

d'où tu sors ça ??
P(X=np) devrait tendre vers 0 quand n tend vers l'infini (en O(1/sqrt(n)) si je me gourre pas ?)

Bonjour,

On a bien ? Donc P(X=np) tend bien vers 0 avec n qui tend vers +oo, et en O() ?

Eh bien, comme dit plus haut, je tire cela du théorème de Moivre-Laplace :

P(X=np), ou plutôt P(X [np-1/2 ; np+1/2[) est très proche de .

De même, P(X [k-1/2 ; k+1/2[) est très proche de . (merci Wiki pour les formules Tex ).

C'est-à-dire que les lois binomiales et lois normales (non centrées non réduites) sont très proches l'une de l'autre (sur une base de rectangle de 1), (par un changement de variable sur l'intégrale), et de plus en plus proches avec n qui tend vers +oo.

Pour s'en convaincre : = 0,39894...
et avec p=0,4, et :
n=30, on a : P(X=np)=0,39545...
n=300, on a : P(X=np)=0,39859...
n=3000, on a : P(X=np)=0,39891...

Si tu remplaçes l'écart type par un autre truc dans l'énoncé du théorème centrale limite, tu obtiens un théorème faux, donc ça veut bien dire que l'écart type est important en général.

Merci. Si tu dis vrai, et je le suppose, cela suffit à répondre à ma question, à savoir que l'écart-type a un rôle privilégié en proba-stats (par rapport aux autres mesures de dispersion). Mais je ne trouve pas le moyen de l'expliquer simplement.
En effet, on m'avait toujours dit (mes professeurs) qu'on prenait l'écart-type plutôt que la moyenne des valeurs absolues des écarts, car cela facilitait les calculs. Or ce n'est pas tout à fait cela...., c'est plus que ça.

[Pseuda]

@Doraki

Peux-tu expliciter dans quel sens le théorème central limite devient faux si on remplace l'écart-type par une autre mesure de dispersion ? Plus aucune convergence, ou bien convergence différente vers une autre loi, par exemple une loi normale biaisée (je ne sais pas si je me fais bien comprendre, ou même si "une loi normale biaisée" a un sens) ?

[Doraki]

le TCL dit que si tu prends une suite (Xn) de variables indépendantes de même loi, d'espérance µ ; et si Sn = somme pour k=1 à n de Xk,
alors la variable aléatoire (Sn - nµ)/sqrt(n) converge en loi vers une variable aléatoire gaussienne centrée en 0.

jusque là personne n'a parlé de mesure des écarts. Quand tu additionnes plein de variables aléatoires identiques, après renormalisation, tu auras toujours un truc proche d'une gaussienne.

L'écart-type sert à savoir exactement de quelle gaussienne centrée en 0 il s'agit.
Parmi toutes les gaussiennes centrées en 0, ce sera celle qui a (je crois) le même écart-type qu'un Xn.
En tout cas si tu veux savoir sur quelle gaussienne tu aterris, ça revient à savoir l'écart-type de Xn, et pas autre chose.

[Pseuda]

Bonjour,

Merci beaucoup Doraki, c'est très clair. Je reprends et corrige mon message précédent (que j'ai supprimé).

Donc, si les Xn suivent une loi de Bernoulli, l'écart-type des Xn étant , la v.a. (Sn-n)/ 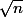converge vers une v.a. de loi normale N(0, p(1-p) ).

Et c'est ce qui explique que, pour une loi binomiale, (Sn-n)/ converge vers une v.a. de loi N(0,1).

Dès lors, si on choisit une autre mesure de dispersion, par exemple, l'écart moyen (moyenne des valeurs absolues des écarts à la moyenne) ' plutôt que pour les Xn, la variable aléatoire (Sn-n)/('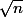) convergerait en loi vers une variable aléatoire qui suit la loi N(0, ).

Par exemple, la loi de Bernoulli a pour écart-type et pour écart moyen 2p(1-p), (sauf erreur), (qui coïncident pour p = 1/2). Dès lors, (Sn-n)/('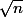) converge vers une v.a. de loi N(0, ) ?

L'écart-type est donc la seule mesure de dispersion ' telle que (Sn-n)/('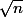) a une loi qui tend vers une loi gaussienne N(0,1), qui s'exprime aussi simplement avec la fonction de densité que l'on connaît ? Donc son rôle est bien privilégié parmi les autres mesures de dispersion.

Cela peut se voir aussi avec le : P(X=k) pour X suivant une loi binomiale, très proche de , d'autant plus proche que n est grand, très visible avec k = (si c'est un entier), formule que je n'ai pas réussi à démontrer rigoureusement...

Ou tout simplement encore, avec le théorème de Moivre-Laplace.

Ouf, j'ai compris, merci encore.

[nuage]

Bonsoir,
pour une justification rapide de l'usage de l’écart-type :
c'est la distance euclidienne au point moyen.

Tu considères une mesure sur n individus. Tu te places dans avec un axe par individu.
La moyenne est alors la projection du point A défini par tes résultats sur la première diagonale (droite vectorielle dirigé par le vecteur (1,1,...,1)).
Et l'écart-type est la distance entre la moyenne et le point A, en prenant comme unité la norme du vecteur (1,1,...,1).

Une vaste part de la statistique relève de la géométrie élémentaire.

[Pseuda]

Bonsoir,
pour une justification rapide de l'usage de l’écart-type :
c'est la distance euclidienne au point moyen.

Tu considères une mesure sur n individus. Tu te places dans avec un axe par individu.
La moyenne est alors la projection du point A défini par tes résultats sur la première diagonale (droite vectorielle dirigé par le vecteur (1,1,...,1)).
Et l'écart-type est la distance entre la moyenne et le point A, en prenant comme unité la norme du vecteur (1,1,...,1).

Une vaste part de la statistique relève de la géométrie élémentaire.

Bonjour,

Je ne comprends pas : une moyenne qui est une projection d'un point ? Peux-tu donner un exemple ?

Une bonne approche du TCL et de l'écart-type :
https://fr.wikipedia.org/wiki/Th%C3%A9o ... ral_limite

Ce qui est certain, c'est que l'écart-type a une affinité avec la loi normale, mais toujours est-il qu'il me paraît très difficile d'en donner une définition convaincante (à part son mode de calcul). Je n'ai rien trouvé sur Internet.

Pourrait-on tenter : si on répétait une expérience aléatoire un grand nombre de fois, l'empilement de ses réalisations convergerait vers une courbe en cloche, appelée loi normale, et cette loi normale est entièrement définie par 2 paramètres : son espérance et son écart-type (resserrement plus ou moins grand des réalisations autour de l'espérance). (Hum).

[Skullkid]

Bonjour,

Comme zygomatique je pense qu'il est utile de penser en termes de moments. Très informellement, le TCL dit que la somme d'un grand nombre de variables iid oublie tous les moments d'ordre 3 ou plus, et que l'info contenue dans les moments d'ordre inférieur est emballée dans une loi normale.

Le fait qu'on utilise souvent l'écart-type comme mesure de dispersion est contingent, même s'il a plein de qualités en sa faveur (l'interprétation géométrique donnée par nuage, le fait qu'il est relativement facile à manipuler dans les calculs, le fait que le TCL parle de lui, ... ). S'il s'agit juste de quantifier la dispersion, l'écart moyen donne une info plus simple à interpréter.

[Sylviel]

Comme dit par Doraki, le TCL te dis que la moyenne empirique de va iid tends vers une gaussienne (à un coeff \sqrt{n} près). Après tu calcul les paramètres de ta Gaussienne comme tu veux. L'espérance c'est pas compliqué (elle est linéaire), et il se trouve que la variance c'est pas compliqué non-plus via l'indépendance. D'autres mesures de la dispersion seraient plus compliquées.

Sinon le choix de l'écart-type c'est un peu la question de "pourquoi minimiser les moindres carré" ? Plusieurs réponses possible à cela :
- sous certaines hypothèses les moindre carré et le maximum de vraisemblance coïncident
- c'est historiquement ce qu'on a choisit
- on sait comment calculer les moindres carrés efficacement
- dans de nombreux domaines les moindres carrés donnent de bons résultats
...

[zygomatique]

et les "moindres carrés" correspond à la distance euclidienne ...

[Sylviel]

Peut-être mais en un sens un peu complexe : d'un côté tu as plusieurs point, de l'autre tu n'en as qu'un. Définir une distance euclidienne naturelle n'est pas si évident.

[Pseuda]

Finalement, tout cela est une coïncidence heureuse. L'écart-type a peut-être été choisi historiquement pour faciliter les calculs, et il se trouve que c'est la mesure de dispersion "naturelle" de la loi normale, qui elle-même est la loi de probabilité la plus "naturelle" lors de la répétition d'une expérience, ce qui est à la base même du calcul de probabilités.

Autre coïncidence (mais ce n'en est peut-être pas une), une fluctuation d'échantillonnage est précise comme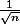 , c'est-à-dire que pour avoir une précision n fois plus grande, il faut un échantillon n² fois plus grand. Et l'écart-type est calculé en faisant la moyenne des carrés des écarts à la moyenne sur n, dont on prend la racine carrée, donc au final, on divise par (alors que l'écart moyen, on divise par n).

Ce qui pose le plus problème, c'est la comparaison avec l'écart moyen. En effet l'écart interquartile ne rend pas compte de la totalité des valeurs (mais de seulement 50%),l'étendue ne rend compte que des 2 valeurs extrêmes, n'en parlons pas ...

Ce qui est paradoxal, c'est que l'écart moyen paraît intuitivement le plus naturel, alors qu'en fait, mathématiquement, c'est l'écart-type qui l'est. Il y a bien sûr la recherche des moindres carrés (qui est étroitement lié à l'écart-type), (mais la recherche des moindres écarts en valeur absolue a aussi son intérêt), l'analogie avec la distance euclidienne, ..., sauf que le lien logique n'est pas évident : c'est la distance la plus courte entre 2 points qui fait que ... ?

[zygomatique]

une moyenne m a même dimension que les données x

l'écart type s aussi

l'écriture (x - m)/s est donc sans dimension .... et a donc un sens ....

[Pseuda]

une moyenne m a même dimension que les données x

l'écart type s aussi

l'écriture (x - m)/s est donc sans dimension .... et a donc un sens ....

Bonjour,

Je ne vois pas ce que tu veux dire par "a même dimension". Dans ce registre, on peut dire aussi que l'écart moyen a même dimension que les données, et donc l'écart-type a même dimension que l'écart moyen. Or ce n'est pas le cas ? L'écart moyen est fonction de n (nombre de valeurs de la série statistique), et l'écart type de .

Si on ne prend que les écarts à la moyenne (ou si on se ramène à une moyenne égale à 0, ce qui revient au même), dans tous les cas : écart moyen = écart-type = (qui est lui-même : ).

Par exemple, si on prend une série : -1 .... (n-2) fois 0 .... 1 ; moyenne = 0, écart moyen = , écart type = . Ce n'est pas la même dimension....

Mais tout cela ne m'avance toujours pas à comprendre pourquoi l'écart-type est si heureux...