Question à propos de l'écart type
79 messages
- Page 3 sur 4 - 1, 2, 3, 4
Crammer Teacher Bags,Trainer Store-Nationwide Gratis Shippin
Nationwide Liberated Shipping INSTRUCTOR bags,carriage purse.100% palpable quality,abstention emancipation,1 week announce to you! ¥³©`¥Á ز¼ ¥³©`¥Á¥Ð¥Ã¥° ¥³©`¥Á ͨØ
Crammer Cram Bags,Coach Store-Nationwide Self-ruling Shippin
Nationwide Available Shipping INSTRUCTOR bags,crammer purse.100% authentic attribute,dissolute articulation,1 week deliver to you! ¥³©`¥Á ز¼ ¥³©`¥Á¥Ð¥Ã¥° ¥³©`¥Á ͨØ
Ok.
Cela étant je ne parle pas de préférence, mais d'existence.
Il me semble qu'il n'existe pas d'estimateurs de l'écart-type réellement sans biais (contrairement à l'espérance et à la variance) : me trompe-je ?
J'illustre ma question sur un exemple.
L'estimateur de la variance) est avec biais.
est avec biais.
Pour le rendre sans biais, lorsque on effectue n expériences indépendantes, on multiplie par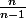 , d'où la considération de
, d'où la considération de ) .
.
OK.
Maintenant, il est naturel de passer de l'estimateur de la variance à celui de l'écart-type en composée avec la racine carrée.
Mais il est faut que}) soit sans biais.
soit sans biais.
Preuve avec cette série de 3 éléments [0,1,2] :
Moyenne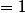 , écart-type
, écart-type 
Imaginons que l'on veuille estimer l'écart-type avec un échantillon à 2 "éléments indépendants" \in [0,1,2]^3) . Alors la moyenne de l'estimateur d'écart-type
. Alors la moyenne de l'estimateur d'écart-type ) est
est  , ce qui n'est pas l'écart-type de [0,1,2] !
, ce qui n'est pas l'écart-type de [0,1,2] !
Cela étant je ne parle pas de préférence, mais d'existence.
Il me semble qu'il n'existe pas d'estimateurs de l'écart-type réellement sans biais (contrairement à l'espérance et à la variance) : me trompe-je ?
J'illustre ma question sur un exemple.
L'estimateur de la variance
Pour le rendre sans biais, lorsque on effectue n expériences indépendantes, on multiplie par
OK.
Maintenant, il est naturel de passer de l'estimateur de la variance à celui de l'écart-type en composée avec la racine carrée.
Mais il est faut que
Preuve avec cette série de 3 éléments [0,1,2] :
Moyenne
Imaginons que l'on veuille estimer l'écart-type avec un échantillon à 2 "éléments indépendants"
Ok.
Cela étant je ne parle pas de préférence, mais d'existence.
Il me semble qu'il n'existe pas d'estimateurs de l'écart-type réellement sans biais (contrairement à l'espérance et à la variance) : me trompe-je ?
J'illustre ma question sur un exemple.
L'estimateur de la variance^2) est avec biais.
est avec biais.
Pour le rendre sans biais (lorsque on effectue n expériences indépendantes), on le multiplie par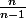 , d'où la considération de
, d'où la considération de ^2) .
.
OK.
Maintenant, il est naturel de passer de l'estimateur de la variance à celui de l'écart-type en composant avec la racine carrée.
Mais il est faux que^2}) soit sans biais.
soit sans biais.
Preuve avec cette série de 3 éléments [0,1,2] : moyenne , écart-type
, écart-type 
Imaginons que l'on veuille estimer l'écart-type avec un échantillon à 2 "éléments indépendants" \in [0,1,2]^3) . Alors la moyenne de l'estimateur d'écart-type
. Alors la moyenne de l'estimateur d'écart-type ) est
est  , ce qui n'est pas l'écart-type de [0,1,2] !
, ce qui n'est pas l'écart-type de [0,1,2] !
Cela étant je ne parle pas de préférence, mais d'existence.
Il me semble qu'il n'existe pas d'estimateurs de l'écart-type réellement sans biais (contrairement à l'espérance et à la variance) : me trompe-je ?
J'illustre ma question sur un exemple.
L'estimateur de la variance
Pour le rendre sans biais (lorsque on effectue n expériences indépendantes), on le multiplie par
OK.
Maintenant, il est naturel de passer de l'estimateur de la variance à celui de l'écart-type en composant avec la racine carrée.
Mais il est faux que
Preuve avec cette série de 3 éléments [0,1,2] : moyenne
Imaginons que l'on veuille estimer l'écart-type avec un échantillon à 2 "éléments indépendants"
Dlzlogic a écrit:Bonsoir,
Il y a deux expressions ou termes qu'il me semble nécessaire de préciser
1- moyenne quadratique
2- biais
Pour moi, l'écart type de la série 0,1,2 est racine(2/(3-1)) = 1.
Tu sais que wikipédia est ton ami... http://fr.wikipedia.org/wiki/Exp%C3%A9rience_al%C3%A9atoire
1- pour la moyenne quadratique, lire http://fr.wikipedia.org/wiki/Moyenne#Moyenne_quadratique
2- pour le biais, lire http://fr.wikipedia.org/wiki/Estimateur_(statistique)#Biais
3- pour l'écart-type, lire http://fr.wikipedia.org/wiki/%C3%89cart_type#D.C3.A9finition
Le 1 que tu calcules est l'estimateur
@leon1789 : Oui en effet ces deux estimateurs de l'écart type sont biaisés, même si l'estimateur de la variance avec n-1 au dénominateur ne l'est pas. Je ne sais pas s'il existe d'estimateur simple non biaisé de l'écart type, mais a priori (à confirmer, les stats ne sont pas mon domaine de prédilection) l'estimateur sans biais de la variance suffit, et le fait d'en prendre la racine carrée sert surtout à mon avis à mieux se représenter les choses (et les estimateurs de l'écart type sont tout de même convergents, si je dis pas de bêtises).
leon1789 a écrit:Tu sais que wikipédia est ton ami...
1- pour la moyenne quadratique
2- pour le biais
Oh non, Wikiperia n'est pas mon ami, et te souviens probablement ce que je t'ai dit à propos de tous ceux qui semblaient avoir comme seule référence un article de Wiki
Quant aux questions, elles étaient posées à Elerinna. De mémoire, c'est la première fois que cette expression est employée dans ce contexte.
Arrête de justifier ton refus de lire les références qu'on te donne par le fait qu'elles ne sont pas à ton goût. Certes, Wikipédia est une référence sujette à caution, mais quand une personne te file un lien Wikipédia, c'est souvent (en tout cas ça a été le cas jusqu'ici dans toutes ces batailles interminables contre ta stupidité) qu'elle estime qu'il explique convenablement un concept que ladite personne maîtrise déjà grâce à d'autres sources. Quand bien même, Doraki, Sylviel et plusieurs autres t'ont filé plusieurs cours complets d'introduction aux proba/stat que tu n'as jamais daigné lire.
Wikipédia n'est peut-être pas ton ami, mais en même temps tu reste sur des définitions erronnées de l'écart-type... Ouvre un bouquin quelconque (y compris le pdf que tu nous a fournit) et lis vraiment ce qui y est écrit si tu n'aimes pas wiki. Tu verras que l'écart-type de la série stat n'est pas ce que tu as calculé...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Bonjour Sylviel,
Si tu fais référence à [0,1,2] moyenne = 1, écart type=sqrt(((0-1)²+(1-1)²+(2-1)²)/(3-1)) = 1.
Quelle est la faute ? Quelle est la bonne réponse ? Pourquoi ?
Si tu fais référence à autre-chose, de quoi s'agit-il ?
Tu verras que l'écart-type de la série stat n'est pas ce que tu as calculé...
Si tu fais référence à [0,1,2] moyenne = 1, écart type=sqrt(((0-1)²+(1-1)²+(2-1)²)/(3-1)) = 1.
Quelle est la faute ? Quelle est la bonne réponse ? Pourquoi ?
Si tu fais référence à autre-chose, de quoi s'agit-il ?
Dlzlogic a écrit:Bonjour Sylviel,
Si tu fais référence à [0,1,2] moyenne = 1, écart type=sqrt(((0-1)²+(1-1)²+(2-1)²)/(3-1)) = 1.
Quelle est la faute ? Quelle est la bonne réponse ? Pourquoi ?
Si tu fais référence à autre-chose, de quoi s'agit-il ?
Je tente ma chance.
Peux-tu calculer la variance de ta série [0,1,2] ?
ev85 a écrit:Je tente ma chance.
Peux-tu calculer la variance de ta série [0,1,2] ?
Bonjour,
"Variance" ne fait pas partie de nom vocabulaire.
J'ai découvert ce terme il y très peu de temps, j'ai appris que c'était le carré de l'écart-type, j'ai appris par le même occasion ce qu'était la co-variance, la bêta-convergence, la sigma-convergence, l'indice de Gini, l'indice de niveau.
Depuis il semble que l'écart-type est la racine carrée de la variance.
Je suppose que la variance a une définition, que je ne connais pas.
Donc, si on me demande de calculer une variance, je calcule un écart-type, et j'élève au carré.
Par ailleurs, ces calculs étant généralement faits sur un grand nombre d'observations, la différence est minime, voire insensible, mais comme on est sur un forum de maths, autant appeler les choses par leur nom.
Si ça intéresse quelqu'un, je peux donner un calcul justificatif qui peut servir de démonstration.
Dlzlogic a écrit:Bonjour,
"Variance" ne fait pas partie de nom vocabulaire.
J'ai découvert ce terme il y très peu de temps, j'ai appris que c'était le carré de l'écart-type, j'ai appris par le même occasion ce qu'était la co-variance, la bêta-convergence, la sigma-convergence, l'indice de Gini, l'indice de niveau.
Depuis il semble que l'écart-type est la racine carrée de la variance.
Je suppose que la variance a une définition, que je ne connais pas.
Donc, si on me demande de calculer une variance, je calcule un écart-type, et j'élève au carré.
Par ailleurs, ces calculs étant généralement faits sur un grand nombre d'observations, la différence est minime, voire insensible, mais comme on est sur un forum de maths, autant appeler les choses par leur nom.
Si ça intéresse quelqu'un, je peux donner un calcul justificatif qui peut servir de démonstration.
J'aurai tenté ma chance...
Dlzlogic a écrit:Je suppose que la variance a une définition, que je ne connais pas.
C'est bien dommage... Tu veux un lien sur wiki ? :lol3:
Dlzlogic a écrit:Donc, si on me demande de calculer une variance, je calcule un écart-type, et j'élève au carré.
Par ailleurs, ces calculs étant généralement faits sur un grand nombre d'observations, la différence est minime, voire insensible, mais comme on est sur un forum de maths, autant appeler les choses par leur nom.
la différence entre quoi et quoi ? Entre un écart-type et la variance ?
Dlzlogic a écrit:Si ça intéresse quelqu'un, je peux donner un calcul justificatif qui peut servir de démonstration.
Une démonstration de quoi ?
leon1789 a écrit:C'est bien dommage... Tu veux un lien sur wiki ? :lol3:
Moi, je préfère cette définition :
Source :II.9 Variance et Covariance
L´ecart type et son carr´e, la variance, repr´esentent l´ecart ou la variation par rapport
`a la moyenne. Ils permettent de quantifier la dispersion des valeurs possibles
par rapport `a la moyenne. Ces notions sont tr`es utilis´ees en calcul des probabilit´es
mais aussi en statistique.
Contrairement à ce qui se dit, je lis, très soigneusement, les cours dont on me donne les références.
Recherches faites, autrefois, cette quantité (variance) était appelée "dispersion". (tien, c'est drôle, ce cours emploie le même mot).
la différence entre quoi et quoi ? Entre un écart-type et la variance ?
Je pense que c'est de l'humour, puisque l'un est la racine carrée de l'autre
Une démonstration de quoi ?
Je parlais de la démonstration de la formule de l'écart-type. Là, je me suis trompé. L'erreur type est une définition,
Si les écarts utilisés sont calculés par différence à la moyenne vraie , le dénominateur est N.
Dans le cas général, ou tout au moins, celui qui nous intéresse, la moyenne vraie n'est pas connue, alors on substitue pour les besoins du calcul [ formule avec dénominateur (N-1)]
je cite :"dont on démontre l'équivalence à la forme théorique. (démonstration que je ne connais pas.)
A propos du sens du terme "biais", j'ai fini par trouver, je crois.
Une série et l'ensemble des valeurs est "sans biais" quand on connait la moyenne. J'emploie habituellement l'expression "valeur vraie" ou "moyenne vraie". Dans ce cas les écarts constatés sont appelés des "écarts vrais", et le dénominateur de l'écart type est N.
Dans le cas de mesures où on ne connait pas la valeur vraie, on emploie le terme mesure avec biais, et les écarts ne sont plus des écarts vrais mais des écarts apparents. Le dénominateur de la formule est (N-1).
Une série et l'ensemble des valeurs est "sans biais" quand on connait la moyenne. J'emploie habituellement l'expression "valeur vraie" ou "moyenne vraie". Dans ce cas les écarts constatés sont appelés des "écarts vrais", et le dénominateur de l'écart type est N.
Dans le cas de mesures où on ne connait pas la valeur vraie, on emploie le terme mesure avec biais, et les écarts ne sont plus des écarts vrais mais des écarts apparents. Le dénominateur de la formule est (N-1).
Dlzlogic a écrit:Moi, je préfère cette définition :II.9 Variance et Covariance
L´ecart type et son carr´e, la variance, repr´esentent l´ecart ou la variation par rapport
`a la moyenne. Ils permettent de quantifier la dispersion des valeurs possibles
par rapport `a la moyenne. Ces notions sont tr`es utilis´ees en calcul des probabilit´es
mais aussi en statistique.
Oui, par rapport à la moyenne, l'écart type est l'écart, la variance est la variation.
Mais c'est quoi l'écart et la variation ?
Dlzlogic a écrit:Je pense que c'est de l'humour, puisque l'un est la racine carrée de l'autre
C'est toi qui a bien écrit que la différence était minime lorsqu'il y a un grand nombre d'observations. Je demande simplement quelle différence car je ne comprends pas de il s'agit.
Dlzlogic a écrit:Je parlais de la démonstration de la formule de l'écart-type. Là, je me suis trompé. L'erreur type est une définition,
Si les écarts utilisés sont calculés par différence à la moyenne vraie , le dénominateur est N.
Dans le cas général, ou tout au moins, celui qui nous intéresse, la moyenne vraie n'est pas connue, alors on substitue pour les besoins du calcul [ formule avec dénominateur (N-1)]
je cite :"dont on démontre l'équivalence à la forme théorique. (démonstration que je ne connais pas.)
Pour moi, un bout de phrase "dont on démontre l'équivalence à la forme théorique" est bien peu pour expliciter tout ça.
Dlzlogic a écrit:Moi, je préfère cette définition :
Source :
Tu n'as pas cité une définition mais un paragraphe qui veut présenter intuitivement la notion.
La définition c'est ce qui vient juste après :
Definition II.28 : Soit X une variable aléatoire réelle de carré intégrable. On définit la variance de X, Var(X), par :
Var(X) = espérance de la variable (X - (espérance de X))²
Ca, c'est une définition de la variance d'une variable aléatoire réelle de carré intégrable.
79 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
