DSE et équations différentielles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 01 Déc 2013, 04:58
par psp » 01 Déc 2013, 04:58
Bonsoir,
Soit
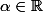
et
=cos(\alpha arcsin (x)))
Je dois déterminer une équation différentielle d'ordre 2 dont f est solution puis un déduire un développement en série entière.
Je cherche cette équation différentielle par tâtonnement en espérant trouver quelque chose, la piste la plus 'valable' que j'ai trouvé étant :
}{(1-x^{2})^{\frac{1}{2}}} (1- \frac{x}{1-x}))
De l'aide ?
Merci d'avance
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 01 Déc 2013, 06:44
par deltab » 01 Déc 2013, 06:44
Bonjour.
psp a écrit:Bonsoir,
Soit
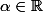
et
=cos(\alpha arcsin (x)))
Je dois déterminer une équation différentielle d'ordre 2 dont f est solution puis un déduire un développement en série entière.
Je cherche cette équation différentielle par tâtonnement en espérant trouver quelque chose, la piste la plus 'valable' que j'ai trouvé étant :
}{(1-x^{2})^{\frac{1}{2}}} (1- \frac{x}{1-x}))
De l'aide ?
Merci d'avance
L'équation différentielle que tu as trouvée ne se prête guère à un DSE
L'idéal pour l'équation différentielle cherchée est qu'elle soit de la forme
y''+B(x)y'+C(x)y=D(x))
où
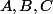
sont des polynômes et

une fonction développable en série entière, si possible déjà connu ou au pire pas difficile à trouver.
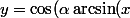))
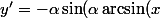)\dfrac{1}{\sqrt{1-x^2}})
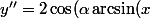)\dfrac{1}{1-x^2}-\alpha\sin(\alpha \arcsin(x))\dfrac{1}{1-x^2}\dfrac{x}{\sqrt{1-x^2}})
Essaies d'écrire

sous la forme
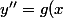y+h(x)y')
,

et

étant des fonctions de

et ramène cette écriture à une forme dont le DSE est simple à exprimer.
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 01 Déc 2013, 15:19
par psp » 01 Déc 2013, 15:19
deltab a écrit:Bonjour.
L'équation différentielle que tu as trouvée ne se prête guère à un DSE
L'idéal pour l'équation différentielle cherchée est qu'elle soit de la forme
y''+B(x)y'+C(x)y=D(x))
où
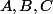
sont des polynômes et

une fonction développable en série entière, si possible déjà connu ou au pire pas difficile à trouver.
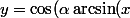))
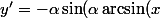)\dfrac{1}{\sqrt{1-x^2}})
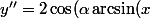)\dfrac{1}{1-x^2}-\alpha\sin(\alpha \arcsin(x))\dfrac{1}{1-x^2}\dfrac{x}{\sqrt{1-x^2}})
Essaies d'écrire

sous la forme
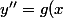y+h(x)y')
,

et

étant des fonctions de

et ramène cette écriture à une forme dont le DSE est simple à exprimer.
Merci pour ce coup de pouce j'ai beaucoup avancé,
J'ai trouvé

Or il dépend de
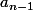
et
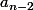
} ((n-2)(n-3) + \alpha^{2}))
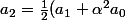)
Je suis censé voir quelque chose pour obtenir a(n) dépendant seulement de n, mais là je vois rien, j'ai peut être fait une erreur de calcul...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Déc 2013, 16:42
par Ben314 » 01 Déc 2013, 16:42
Tu as vérifié le y'' de deltab ? (j'ai l'impression qu'il y a une erreur de signe au début)
Perso, après calculs, je trouve

c'est à dire
a_n=\big((n-2)(n-3)+(n-2)-\alpha^2\big)a_{n-2})
pour tout

Donc
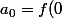=1)
;
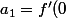=0)
et, pour

,
^2-\alpha^2}{n(n-1)}a_{n-2})
Ce qui semble correspondre à ce que trouve
wolframQui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 01 Déc 2013, 16:57
par Sa Majesté » 01 Déc 2013, 16:57
Ben314 a écrit:Tu as vérifié le y'' de deltab ? (j'ai l'impression qu'il y a une erreur de signe au début)
+1
J'ai aussi des doutes sur
psp a écrit:J'ai trouvé

Or il dépend de
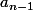
et
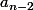
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 01 Déc 2013, 17:38
par psp » 01 Déc 2013, 17:38
Ben314 en reprenant depuis le début je retombe bien sur ton résultat merci
Maintenant wolfram me donne une solution de récurrence avec des fonctions gamma, je vais voir ça...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 01 Déc 2013, 17:48
par Sa Majesté » 01 Déc 2013, 17:48
Ben314 a écrit:Perso, après calculs, je trouve

Moi j'avais trouvé

EDIT : non c'est bon :marteau:
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 01 Déc 2013, 18:20
par psp » 01 Déc 2013, 18:20
Je n'arrive pas à me débarrasser des fonctions gamma contenant a, puisque a appartient à R...
[url=http://www.wolframalpha.com/input/?i=u%280%29+%3D+1%2C+u%281%29+%3D+0%2C+u%28n%29%3D%28%28n-2%29^2+-+a^2%29%2F%28n%28n-1%29%29+u%28n-2%29]Wolfram[/url]

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Déc 2013, 18:41
par Ben314 » 01 Déc 2013, 18:41
Je sais pas sous quelle forme tu veut obtenir

, mais perso, j'aurais écrit (réccurence "triviale") que,
pour n pair, on a :
^2-\alpha^2}{n(n-1)}a_{n-2}=...=\frac{(n-2)^2-\alpha^2}{n(n-1)}\times\frac{(n-4)^2-\alpha^2}{(n-2)(n-3)}\times\dots\times\frac{2^2-\alpha^2}{4\times 3}\times\frac{0^2-\alpha^2}{2\times 1}a_0)
(4^2-\alpha^2)...((n-2)^2-\alpha^2)}{n!})
et ça m'aurais paru suffisant...
Ca montre en particulier que, si

est un entier pair (positif ou négatif) alors les

sont nuls à partir d'un certain rang ce qui signifie que f est un polynôme en x.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 02 Déc 2013, 00:58
par deltab » 02 Déc 2013, 00:58
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
