La double somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 19 Déc 2013, 11:52
par Dante0 » 19 Déc 2013, 11:52
Bonjour,
Dans le cadre d'un exercice, je fais face à une expression de cette forme :
 + \bigsum_{i} \bigsum_{j} cov(X_i,X_j))
avec j différent de i
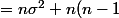p\sigma^2)
Sachant que
 = p\sigma^2)
Du coup d'ou vient le
)
?
Merci
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 19 Déc 2013, 11:56
par lionel52 » 19 Déc 2013, 11:56
c'est le nombre de termes (i,j) avec i différent de j et i et j compris entre 1 et n :)
en gros c'est n² - n
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 19 Déc 2013, 14:17
par Dante0 » 19 Déc 2013, 14:17
lionel52 a écrit:c'est le nombre de termes (i,j) avec i différent de j et i et j compris entre 1 et n

en gros c'est n² - n
Je te suis pas du tout la :doh:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Déc 2013, 14:38
par Sylviel » 19 Déc 2013, 14:38
Imagine que tu as un tableau de termes (i pour les lignes, j pour les colonnes).
Puisque tous tes termes ont la même valeurs il te suffit de savoir combien de termes tu as.
Tu les as tous (tu sommes sur tous les i et j) sauf ceux tel que i=j. Tu en as donc n² (le nombre de termes dans le tableau) - n (le nombre de termes sur la diagonale), ou en core n(n-1).
Chaque fois que tu as des manipulation de double somme essaie de visualiser sur un tableau, ça aide :zen:
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 19 Déc 2013, 14:56
par Dante0 » 19 Déc 2013, 14:56
Sylviel a écrit:Imagine que tu as un tableau de termes (i pour les lignes, j pour les colonnes).
Puisque tous tes termes ont la même valeurs il te suffit de savoir combien de termes tu as.
Tu les as tous (tu sommes sur tous les i et j) sauf ceux tel que i=j. Tu en as donc n² (le nombre de termes dans le tableau) - n (le nombre de termes sur la diagonale), ou en core n(n-1).
Chaque fois que tu as des manipulation de double somme essaie de visualiser sur un tableau, ça aide :zen:
Mais en fait ca donne toujours ca ? C'est une sorte de formule ?
Les termes en diagonales c'est les i=j c'est cela ?
Quand tu dis que tous les termes ont la même valeurs, ca veut pas dire que i =j ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Déc 2013, 15:08
par Sylviel » 19 Déc 2013, 15:08
Ben dans une matrice n x n il y a toujours n(n-1) termes non diagonaux.
Tu as un échantillon de taille n. Tu as ta matrice de covariance de taille n x n.
L'élément (i,j) de ta matrice c'est cov(Xi,Xj).
Si i=j tu as cov(Xi,Xj)=Cov(Xi,Xi)=Var(Xi).
D'après ce que tu as écrit j'imagine que tu calcule
 = \sum_{i=1}^n \sum_{j=1}^n cov(X_i,X_j) <br />= \sum_{i=1}^n Var(X_i) + \sum_{i \neq j} cov(X_i,X_j))
Donc tu veux sommer tous tes termes de la matrice de covariance, et tu mets d'un côté ceux de la diagonale (quand i=j) et de l'autres les autres. Ensuite tu nous as dis que toutes les variance était égales, donc c'est n fois l'une d'entre elle, et que toutes les covariances était égale (à p sigma²) donc c'est n(n-1) fois l'une d'entre elle.
C'est clair ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 19 Déc 2013, 15:15
par Dante0 » 19 Déc 2013, 15:15
Sylviel a écrit:Ben dans une matrice n x n il y a toujours n(n-1) termes non diagonaux.
Tu as un échantillon de taille n. Tu as ta matrice de covariance de taille n x n.
L'élément (i,j) de ta matrice c'est cov(Xi,Xj).
Si i=j tu as cov(Xi,Xj)=Cov(Xi,Xi)=Var(Xi).
D'après ce que tu as écrit j'imagine que tu calcule
 = \sum_{i=1}^n \sum_{j=1}^n cov(X_i,X_j) <br />= \sum_{i=1}^n Var(X_i) + \sum_{i \neq j} cov(X_i,X_j))
Donc tu veux sommer tous tes termes de la matrice de covariance, et tu mets d'un côté ceux de la diagonale (quand i=j) et de l'autres les autres. Ensuite tu nous as dis que toutes les variance était égales, donc c'est n fois l'une d'entre elle, et que toutes les covariances était égale (à p sigma²) donc c'est n(n-1) fois l'une d'entre elle.
C'est clair ?
D'accord.
Et si j n'était pas différent de i on aurait eu simplement n² ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Déc 2013, 15:26
par Sylviel » 19 Déc 2013, 15:26
oui si tu sommes sur i et j sans conditions et que tous les termes sont égaux alors c'est n² fois la valeur d'un terme.
Mais ici tu as deux valeurs différentes : sur la diagonale, et ailleurs.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 19 Déc 2013, 15:33
par Dante0 » 19 Déc 2013, 15:33
Sylviel a écrit:oui si tu sommes sur i et j sans conditions et que tous les termes sont égaux alors c'est n² fois la valeur d'un terme.
Mais ici tu as deux valeurs différentes : sur la diagonale, et ailleurs.
OK merci

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités