Double somme

[Ellhaym]

Bonjour pourrait on m'expliquer comme à un enfant XD pourquoi :

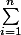
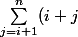équivaut à

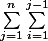(i+j)

Merci à vous

[mathelot]

Bonjour pourrait on m'expliquer comme à un enfant XD pourquoi :

A priori, pour i fixé, la somme de droite , l'indice j variant,
est la somme des termes d'une progression arithmétique

on a une formule pour l'évaluer

[mathelot]

1ère méthode (très bovine)

progression arithmétique


polynôme de Bernoulli


même principe pour la seconde somme..

[Ellhaym]

Oui certes, mais mon problème vient du "trafic" d'indice et du "j-1" dont j'ignore l'origine

[Ptiboudelard]

Oui certes, mais mon problème vient du "trafic" d'indice et du "j-1" dont j'ignore l'origine

ben, de manière grossière ... quand i=1, la seconde somme commence à 2, quand i=2, la seconde somme commence à 3 etc ... donc j ayant toujours 1 de plus, alors de j= 1 à i, on a donc 1 de moins ... d'où le (j-1) ... ahah c'est barbare et pas du mathématique ^^ désolé ... je sors ! :stupid:

[Ellhaym]

C'est comme ça que j'aime les Maths XD, merci à vous tous

[girdav]

On représente l'ensemble de sommation (peu importe ce que l'on somme, ici le fait que ce soit des 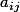ne nous perturberait pas plus que cela) par des points. Ces points vont former une sorte de triangle.
Dans un cas on le balaie horizontalement : on somme sur une ligne, puis on prend la somme des lignes et dans l'autre verticalement : on somme sur les colonnes puis on prend la somme des colonnes.

[Ellhaym]

Je vois ce que tu veux dire, il m'arrive de tracer le triangle dans le cas de sommes partielles afin de vérifier si je ne me trompe pas dans la transformation d'indice

[girdav]

Voilà, pas de bourbakisme. C'est toujours bon de se représenter la situation autant que possible.