Donner des équiavlents simples de ...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 12:37
par pouik » 09 Sep 2007, 12:37
Bonjour,
Pourriez vous m'aider à donner des équivalents simples de :
1.
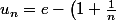^n)
2.
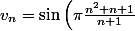)
3.
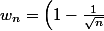^n)
Pour la 2. je trouve
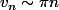
.
Pour la 1. je vois juste que
^n \sim e)
mais l'erreur consisteriat d'en déduire que

, voilà sinon je vois pas comment faire.
Pour le 3., je n'y arrive pas non plus.
Merci d'avance pour votre aide.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Sep 2007, 12:38
par fahr451 » 09 Sep 2007, 12:38
bonjour
1) pousse le dl de ln (1+1/n) à l'ordre 2
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 09 Sep 2007, 12:41
par cesar » 09 Sep 2007, 12:41
pouik a écrit:Bonjour,
Pourriez vous m'aider à donner des équivalents simples de :
1.
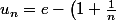^n)
2.
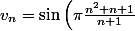)
3.
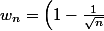^n)
Pour la 2. je trouve
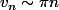
.
Pour la 1. je vois juste que
^n \sim e)
mais l'erreur consisteriat d'en déduire que

, voilà sinon je vois pas comment faire.
Pour le 3., je n'y arrive pas non plus.
Merci d'avance pour votre aide.
lorsque n tend vers qu'elles valeurs ??? sans cette precision, il est impossible faire quoique ce soit... :briques:
pour le 3, si n tend vers l'infini,
)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 09 Sep 2007, 12:43
par Joker62 » 09 Sep 2007, 12:43
Apparemment c'est des suites donc bon, on va dire +oo
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 12:56
par pouik » 09 Sep 2007, 12:56
Je trouve que :
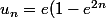 + \circ (qqchose))
donc :

non ??
PS : les équivalents sont en

, on m'avait appris que pour les suites (i.e. quand la variable prend des valeurs entières), alors forcément les équivalents sont en

, mais bon... :zen:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Sep 2007, 13:21
par fahr451 » 09 Sep 2007, 13:21
non c'est faux pour le a)
exp [nln (1+1/n)] = exp1 exp[-1/2n +0(1/n) ]
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 13:29
par pouik » 09 Sep 2007, 13:29
ah oui, en fait c'est :

non ??
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Sep 2007, 13:37
par fahr451 » 09 Sep 2007, 13:37
non
lis ce que j'ai écrit
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 13:43
par pouik » 09 Sep 2007, 13:43
Oui mais on cherche un équivalent de :
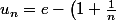^n)
Sinon j'ai fait comme vous mis à part que j'ai factoriser par

, cf. post de 13h56.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Sep 2007, 13:44
par fahr451 » 09 Sep 2007, 13:44
moi aussi
exp 1 = e
exp (-1/(2n) ) = ?
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 13:59
par pouik » 09 Sep 2007, 13:59
exp(-1/(2n)) = exp(-2n)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Sep 2007, 13:59
par fahr451 » 09 Sep 2007, 13:59
ah
non non
exp(-x) = 1/exp(x) et rien d 'autre
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 14:04
par pouik » 09 Sep 2007, 14:04
Oups.... :hum: :hum:
on a donc :
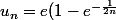)
Or
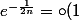)
donc

non ?? :triste:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Sep 2007, 14:05
par fahr451 » 09 Sep 2007, 14:05
pas plus
repars de ma ligne si tu veux bien
exp(h) = 1+h +0(h) h->0
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 14:24
par pouik » 09 Sep 2007, 14:24
fahr451 a écrit:non c'est faux pour le a)
exp [nln (1+1/n)] = exp1 exp[-1/2n +0(1/n) ]
donc je dois faire un developpement limité de exp à partir de ca ?? c'est ce que vous me demandez car je suis pas sur d'avoir bien interpreter votre dernier post.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Sep 2007, 14:25
par fahr451 » 09 Sep 2007, 14:25
ben oui c'est ça
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 09 Sep 2007, 14:42
par emdro » 09 Sep 2007, 14:42
pouik a écrit:Pourriez vous m'aider à donner des équivalents simples de :
2.
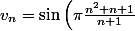)
Pour la 2. je trouve
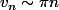
.
Bonjour
Comme un sinus est entre -1 et 1, j'ai des difficultés à croire que
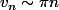
...
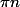
tendant vers l'infini...
NB:
 \sim X)
au voisinage de 0 uniquement.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 14:47
par pouik » 09 Sep 2007, 14:47
On a donc :
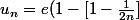 + \circ (\frac{1}{n}))
soit :

non ??
Sinon pour

comment fait-on dans la mesure où on ne connait pas d'équivaloent de sin ailleurs qu'au voisinage de

.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Sep 2007, 14:53
par fahr451 » 09 Sep 2007, 14:53
le e et le 1/2 ont disparu....
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 09 Sep 2007, 14:57
par pouik » 09 Sep 2007, 14:57
fahr451 a écrit:le e et le 1/2 ont disparu....
bah on m'a appris à mettre les équivalents les plus simples possibles et comme bien sur :

, le tour est joué.
non ??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
.
mais l'erreur consisteriat d'en déduire que
, voilà sinon je vois pas comment faire.