Domaine de définition d'une fct a 2 variables

[jay3141516]

la fonction est la suivante
f(x,y) =

Ce que j'ai trouvé,

Df = { (x,y) c R² / 4-x²-y² >0 }

alors
[CENTER]4-x²-y² > 0
y² < 4-x²[/CENTER]
il y a deux reponses la alors j'ai mis
[CENTER]-sqrt(4-x²) < y < +sqrt(4-x²)[/CENTER]

Maintenant j'ai trouvé le domaine pour Y, mais pour X comment je peut faire? je suis bloqué!

Merci

[Sake]

Salut,

la fonction est la suivante
f(x,y) =

Ce que j'ai trouvé,

Df = { (x,y) c R² / 4-x²-y² >0 }

alors
[CENTER]4-x²-y² > 0
y² < 4-x²[/CENTER]
il y a deux reponses la alors j'ai mis
[CENTER]-sqrt(4-x²) < y < +sqrt(4-x²)[/CENTER]

Maintenant j'ai trouvé le domaine pour Y, mais pour X comment je peut faire? je suis bloqué!

Merci

Tout simplement, tu aurais pu écrire x² + y² < 4, qui est l'équation de la boule ouverte, dans R², de rayon 2.

Et c'est terminé.

[jay3141516]

Salut,

Tout simplement, tu aurais pu écrire x² + y² < 4, qui est l'équation de la boule ouverte, dans R², de rayon 2.

Et c'est terminé.

Désolé mais j'ai pas compris, pourquoi on a tiré y pour trouver y² < 4-x²
pourquoi on peut pas faire ça a x aussi? ca va nous donner
x² < 4 - y²

c'est ca ce qui me perturbe!

[Ben314]

Salut,
Le petit "détail" à comprendre, c'est qu'un disque, c'est pas un rectangle donc que tu risque pas d'exprimer que (x,y) est dans un disque à l'aide d'inégalités a0}[/TEX][/U] (donc -2<x<2)

[jay3141516]

[quote="Ben314"]Salut,
Le petit "détail" à comprendre, c'est qu'un disque, c'est pas un rectangle donc que tu risque pas d'exprimer que (x,y) est dans un disque à l'aide d'inégalités a0}[/TEX][/U] (donc -20 et pas x²+y²<4 pour trouver -2<x<2! je ne comprends pas entièrement pourquoi, mais c'est juste.
https://www.wolframalpha.com/input/?i=4-x%C2%B2-y%C2%B2+%3E0

[Ben314]

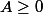
Simplement parce qu'on m'a appris au collège, pour que existe, ben faut que donc quand j'écrit , quelque soit le contexte, je précise qu'il faut que (ou je vérifie que l'énoncé implique cette inégalité)

[jay3141516]

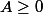
Simplement parce qu'on m'a appris au collège, pour que existe, ben faut que donc quand j'écrit , quelque soit le contexte, je précise qu'il faut que (ou je vérifie que l'énoncé implique cette inégalité)

Merci infiniment! :++: