Continuité fct à 2 variables

[zygomatique]

tu as très bien résumé ton "charabia" et parfaitement synthétisé mon idée

[Pseuda]

Tu pourrait me donner un vague début de définition traduisant le fait que "f(x) tend vers l'infini lorsque x->1 plus vite que g(x) ne tend vers l'infini lorsque x->oo" ?

Bonjour,

Je voulais dire par là, bien que cela n'ait aucun rapport avec le sujet, mais cela m'y fait penser, que pour une même valeur k de l'ordonnée pour ces 2 fonctions, la croissance de la fonction 1/(1-x) en son point d'ordonnée k (sa dérivée), est plus forte que celle de la fonction e^x en son point d'ordonnée k.

Au point d'ordonnée y pour chacune des 2 courbes, avec y = e^x1 = 1/(1-x0), on a : 1/(1-x0)^2 (dérivée de 1/(1-x) en x0) > 1/(1-x0) = e^x1 (dérivée de e^x en x1).

Et ceci bien qu'on parle de la croissance exponentielle comme d'une croissance explosive..., elle augmente moins vite, à ordonnée égale, que la fonction inverse (la puissance du 0 au dénominateur). Cela me turlupine depuis un moment.

[Ben314]

Au départ, j'avais rien compris, mais finalement, je crois que je comprend :
Pour tenter de comparer les "vitesses de divergence" de deux fonctions f et g qui tendent vers +oo, mais pas pour les mêmes valeurs de x, tu compare f'(x1) et g'(x2) où x1 et x2 sont tels que f(x1)=g(x2)=y "très grand".
Donc ça revient en fait à comparer les fonction F=f'of^(-1) et G=g'og^(-1) (dépendant toute les deux de y) lorsque y->oo.
Sauf qu'au fond, si tu connait F (ou G) et que tu cherche à récupérer f (ou g), ben ce que tu as sous les yeux, c'est une équation différentielle f'=Fof et, vu les différences de départ des fonction f et g, les équations différentielles f'=Fof et g'=Gog ont des solutions de nature différentes : pour f'=Fof, il va exister des solutions prolongeable autant qu'on veut (i.e. définies sur du [xo,+oo[) alors que pour la deuxième, on ne pourra pas prolonger autant qu'on veut : toute les solution de l'équa-diff. seront définies sur du [x0,b[ et tendrons vers +oo lorsque x tend vers b. Et cela signifie bien entendue que G tend vers +oo "trop vite" ce qui "bloque" les solutions de l'équa. diff. et les empéche de dépasser un certain seuil critique (en terme physique, le truc étudié va "exploser" au sens propre du terme au bout d'un certain temps alors que pour la 1ère équa-diff, il va "uniquement" augmenter indéfiniment)
Exemple :
F(y)=y => l'équa. diff. f'=f a pour solutions f(x)=lambda.exp(x) définie sur [xo,+oo[
G(y)=y² => l'équa. diff. g'=g² a pour solution g(x)=1/(b-x) définie sur [x0,b[ et non prolongeable ensuite (modulo que la condition initiale soit de la forme g(xo)=yo avec yo>0 pour que b>xo)

Bref, en résumé, ton laïus, au fond, ça consiste à dire que, si une fonction est définie sur [xo,+oo[, même si elle croit extraordinairement vite, ben elle croit moins vite qu'une fonction définie sur [xo,b[ est qui tend vers +oo lorsque x->b : ça me semble effectivement... assez vrai...

[chan79]

Pour montrer que f n'est pas continue en (0,0):
Soit réel strictement positif quelconque
On peut montrer qu'il existe un point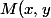 à l'intérieur du disque de centre (0,0) et de rayon tel que

Si M(x,y) est un point du segment rouge d'extrémités et , on a
on pose
L'étude cette fonction montre que f(x) tend vers quand tend vers qui est compris entre 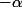et 0.

[Pseuda]

Bonjour,

@Ben314,
Merci. Je comprends ce que tu dis, mais je ne cherche pas à résoudre une équation différentielle.
Cela m'étonne simplement que dans les modèles économiques, physiques, biologiques, dans les manuels scolaires, ... , on parle toujours d'une croissance exponentielle comme la plus grande qui soit, alors que la fonction inverse croit plus vite, dans une certaine limite de la variable, je te l'accorde, mais moyennant une homothétie on peut déplacer cette limite autant qu'on veut.

Mais à la réflexion, il doit y avoir des modèles qui utilisent une borne et dont l'augmentation d'une grandeur est inversement proportionnelle à une autre qui tend vers cette borne. Par exemple, taux de marge = (prix de vente - prix d'achat) / prix d'achat : si le prix de d'achat tend devient nul, le taux de marge tend vers l'infini. Mais ceux-là sont passés sous silence.

Cela m'étonne, tout simplement.

@Chan79,
Est-ce que dans Geogebra (car je suppose que tes jolies courbes proviennent de ce logiciel), on peut visualiser des surfaces dans l'espace ordinaire ? Je serais curieuse de voir la tête de la surface z = xy/(x^2+y).

[chan79]

Je serais curieuse de voir la tête de la surface z = xy/(x^2+y).

les grapheurs ont du mal à calculer, comme on pouvait s'y attendre.






Pour l'image juste au dessus, il suffit d'aller sur le site http://www.archimy.com/
de taper z=x*y/(x^2+y)
et de cliquer sur calculate.
On peut faire pivoter la figure avec la souris.
On visualise la discontinuité aux points (x,-x²)
Pas mieux avec scilab:

Avec mathlab ou autre ?

[zygomatique]

avec le logiciel graphcalc (gratuit) et on peut faire des rotation autour des axes

image.jpg (27.72 Kio) Vu 491 fois

[Pseuda]

Bonsoir,

Merci beaucoup à vous deux. En effet, ce n'est pas évident...

Et on n'a pas la possibilité de visualiser la surface avec la condition de départ : z = 0 pour x²+y = 0.
Je m'attendais à un gouffre au bord d'une falaise le long de la parabole y = - x², et j'imagine que ces pointes le long de cette courbe décrivent l'affolement (bizarre) de z au bord de x²+y=0. (je n'ai pas le temps d'étudier cette surface).

@Chan, comment fait-on pour faire tourner l'image avec la souris, avec archimy ?

[chan79]

comment fait-on pour faire tourner l'image avec la souris, avec archimy ?

Tu déplaces la souris en maintenant la pression sur le bouton gauche
Sinon, c'est plus facile de faire des coupes:
pour y=-2
g(x)=f(x,-2)=-2x/(x²-2)
quand x tend vers par valeurs supérieures, g(x) tend vers

[Ben314]

@Pseuda : pour répondre à ton post. de hier, je parlais d'équa. diff. du fait que la méthode que tu avais employé pour comparer des "vitesses de divergence" de fonctions qui ne divergent pas au même endroit, au fond, ça revenait (plus ou moins) à ça.

Sinon, effectivement, concernant la fameuse "croissance exponentielle" qui est "très grande" il faudrait rajouter "parmi les fonctions définies sur du [xo,+oo[" mais ça me semble quand même clair que c'est sous entendu.

Et qu'on puisse trouver des fonctions définie uniquement sur du [xo,b[ qui "croissent plus vite" (*) que des exponentielles, perso. ça ne m'étonne pas trop et ce que je voulais te signaler avec mes équa.diff., c'est que justement, si, partant d'un certain x=x0, on a une fonction qui "croit bien plus vite que de l'exponentielle", alors elle n'atteindra jamais x=+oo vu qu'elle sera "égale à +oo" avant d'avoir atteint x=+oo.
Alors que la fonction exponentielle, bien que croissant "très vite", ne crois pas assez vite pour atteindre l'infini avant que x lui même n'atteigne l'infini.
Je sais pas si c'est super clair mon truc : j'essaye juste de t'expliquer que ça me semble "bien normal" qu'un truc qui tend vers +oo lorsque x->b, forcément, il "monte plus vite" qu'un truc qui tend vers l'infini lorsque x->oo.

(*) En un certain sens du terme "croitre plus vite", mais tu lui a effectivement donné un sens qui me parrait tout à fait valable.

[Pseuda]

Bonsoir,

Merci à tous. Pas très harmonieuse comme surface.

@Ben314. Je vois ce que tu veux dire. Merci.

[Ben314]

Bonsoir,
Merci à tous. Pas très harmonieuse comme surface.

C'est pas particulièrement étonnant vu que justement la fonction est discontinue et que le logiciel de "trace" fait souvent des "approximations affine" entre les différents points calculé. Et lorsque deux points sont "de part et d'autre" d'une discontinuité, ça fait forcément un truc louche.

En plus, sur les tracés çi dessus, il y en a plusieurs où, clairement, l'utilisateur a laissé le logiciel choisir tout seul l'échelle sur l'axe des z ce qui, dans un cas pareil, n'est pas bien malin : l'ordi. va évidement trouver des points avec des z immenses (vu que f->oo pour certaines valeurs de x et y) donc il va prendre une échelle immense sur l'axe des z et avec cette échelle là, la partie "régulière" de la fonction, on la verra pas vu qu'elle est totalement "aplatie" et par contre, ce qu'on verra très bien, c'est les approximation (foireuses) tentées par l'ordi. pour créer une surface permettant de rejoindre les points ayant des z extrêmement grands.

[Pseuda]

Ah, c'est pour ça que la surface est toute aplatie en dehors de la discontinuité. C'est vrai que l'échelle des x va jusqu'à 300 et 400 selon les graphiques pour y et z variant entre -1 et 1 (si je comprends bien).

[chan79]

c'est plus facile de visualiser des coupes de la surface par des plans d'équation y=k
la courbe rouge donne z en fonction de x.
on visualise la discontinuité en (x,k) si x²+k=0 (si k est strictement négatif)


pour déplacer le plan de coupe: https://www.geogebra.org/m/knufFMYH

[Ben314]

C'est effectivement plus visuel, mais je pense (à vérifier...) que ça serait aussi assez visuel si on faisait un dessin en 3d avec le même intervalle pour z que sur ton dessin, c'est à dire [-4,4] et pas du [-300,300] comme sur le premier dessin donné par chan dans le post du 06 Nov 2016 12:10 ou pire, le [-500,500] du 3em dessin du même post.

Qui fait un test ?
(J'ai testé quelques liens donné et j'ai constaté avec surprise (et un peu de stupeur...) que certains logiciels ne proposent pas de choisir soi même l'intervalle d'affichage des z)

[chan79]

[-4,4] au lieu de [-300,300]

ça ne change rien
z grimpe trop vite, sans doute


le site: http://wims.unice.fr/wims/wims.cgi?session=3UE42DB2D4.2&+lang=fr&+module=tool%2Fgeometry%2Fanimtrace.fr
(choisir surfaces explicites)

[chan79]

je ne sais pas ce que j'avais fichu avec geogebra
ça marche pourtant bien

[Ben314]

Effectivement.
Avec le même logiciel, en prenant -1<z<1, une "densité" de 70 x 70, une résolution de 600x600 et en faisant tourner le dessin, on voit vaguement quelque chose de pertinent (c'est principalement la densité qui rentre en ligne de compte).
Le problème du logiciel en question, c'est que lorsque qu'il doit tracer le segment (en rouge) reliant (x1,y1,z1) à (x2,y2,z2) si jamais z1 ou z2 sort de l'intervalle défini pour les z alors il ne trace absolument rien.
Je pense que le "rendu" serait déjà pas mal meilleur s'il traçait la partie du segment qui correspond a l'intervalle demandé pour z.

EDIT : j'avais pas vu le deuxième message de chan lorsque j'ai répondu : ce message répond a l'avant dernier message et pas au dernier.

[Pseuda]

Les coupes avec geogebra sont intéressantes. Avec y>0, la surface est presque plane, légèrement gondolée (selon les x positifs ou négatifs), et de plus en plus avec y qui grandit, et avec y<0, elle éclate en 3 morceaux infinis qui s'éloignent les uns des autres avec y qui diminue.