Continuité fct à 2 variables

[diracb]

bonjour,
je dois montrer que f n'est pas continue en (0,0) avec f:
f(x,y) = xy/(x^2+y) si le denominateur est différent de 0
= 0 sinon.
mais je ne vois pas pourquoi.
si qqun à une idée, je suis preneur. merci;

[zygomatique]

salut

que vaut f(x, y) quand y = -x^2 ?

[diracb]

oh le boulet que je suis... merci.

[Pseuda]

Oui mais la fonction x^2 y / (x^2+y) serait, elle, continue en (0,0) bien que le dénominateur s'annule pour y = - x^2. Cette justification ne me paraît pas la bonne.

[zygomatique]

prenons alors y = -x^2 + x^{100} ou plus généralement y = -x^2 + o(x^2)

...

mais bon plus simplement f n'est pas définie sur D = {x, y) / y = -x^2} donc f n'est pas définie en (0, 0)

et même si on pose f(0, 0) = 0 il y a un pb lorsque x se rapproche de (0, 0) et de D ...

[Ben314]

mais bon plus simplement f n'est pas définie sur D = {x, y) / y = -x^2} donc f n'est pas définie en (0, 0)

ben... si vu que l'énoncé précise clairement que f est nulle (donc existe !!!) lorsque y+x²=0.

[Pseuda]

prenons alors y = -x^2 + x^{100} ou plus généralement y = -x^2 + o(x^2)

...

mais bon plus simplement f n'est pas définie sur D = {x, y) / y = -x^2} donc f n'est pas définie en (0, 0)

et même si on pose f(0, 0) = 0 il y a un pb lorsque x se rapproche de (0, 0) et de D ...

Bonjour,

f est bien définie sur D = {x, y) / y = -x^2} ? D'après sa définition, f(x,y) = 0 pour (x,y) appartenant à D (oups je répète ce que dit Ben314).

Donc suivant la courbe y = - x², f = 0, donc sa limite est 0, et suivant R²- D, cette justification ne tient plus.

[Pseuda]

Re,

A vrai dire, j'ai même l'impression que cette fonction est continue en (0,0). En effet, suivant R² - D, le x² est dénominateur est négligeable devant le y, et il ne reste plus que : |xy| / |y| = |x|.

Autrement dit : , donc la fonction tend vers 0 quand (x,y) tend vers (0,0), avec (x,y) dans R²- D aussi.

Est-ce une erreur d'énoncé, ou me trompé-je ?

[zygomatique]

mais bon plus simplement f n'est pas définie sur D = {x, y) / y = -x^2} donc f n'est pas définie en (0, 0)

ben... si vu que l'énoncé précise clairement que f est nulle (donc existe !!!) lorsque y+x²=0.

certes mais il y a ensuite une dernière phrase pour revenir à l'énoncé ....

[zygomatique]

Re,

A vrai dire, j'ai même l'impression que cette fonction est continue en (0,0). En effet, suivant R² - D, le x² est dénominateur est négligeable devant le y, et il ne reste plus que : |xy| / |y| = |x|.

Autrement dit : , donc la fonction tend vers 0 quand (x,y) tend vers (0,0), avec (x,y) dans R²- D aussi.

Est-ce une erreur d'énoncé, ou me trompé-je ?

si y est négatif et |y| > x^2 je ne crois pas qu'on aie |x^2 + y| > |y|

ou encore y < x^2 + y < 0 => 0 < |x^2 + y| < |y| et on ne peux pas utiliser la majoration que tu fais ...

c'est vrai si y >= 0 par contre et pour {y >= 0} f est continue en 0 ...

[Pseuda]

Bonjour,

Oui, je me suis rendue de mon erreur juste après. Donc f est continue sur R x [0, +oo [, mais pas sur R x ] -oo, 0].

[Ben314]

La preuve de la non continuité en (0,0), zygomatique l'a donnée (en bleu) :

prenons alors y = -x^2 + x^{100} ou plus généralement y = -x^2 + o(x^2)
...
mais bon plus simplement f n'est pas définie sur D = {x, y) / y = -x^2} donc f n'est pas définie en (0, 0)
et même si on pose f(0, 0) = 0 il y a un pb lorsque x se rapproche de (0, 0) et de D ...

Par contre, ce qui suis le "plus simplement...", c'est faux.

[Pseuda]

La preuve de la non continuité en (0,0), zygomatique l'a donnée (en bleu) :

prenons alors y = -x^2 + x^{100} ou plus généralement y = -x^2 + o(x^2)...

Bonjour,

Cela ne me paraît toujours pas convaincant. Si on pose : , avec 0(1) une fonction qui tend vers 0 avec x, on obtient :

, soit une forme indéterminée .

[Ben314]

Effectivement, son o(x^2) final n'est pas tout à fait bon, mais le de départ, lui, il est bon.

Si on prend avec pour 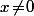(pour ne pas tomber sur le cas particulier), alors et pour que ça ne tende pas vers 0 lorsque x->0, il suffit de prendre (donc par exemple ou ), et , c'est pas suffisant.

[Pseuda]

Oui il suffit de prendre o(x^3). C'est une bonne technique, à retenir.

En fait c'était la fonction x^2y/(x^2+y), avec les mêmes hypothèses, dont je n'arrive pas à démontrer qu'elle est continue en (0,0), alors que visiblement, elle l'est.

[Ben314]

On peut pas dire que ça change grand chose de mettre un x² à la place du x au numérateur :
Si alors qui, si est un , ne tend pas vers 0 lorsque x->0.

[Pseuda]

Bon alors je risquais pas de démontrer qu'elle l'était. C'est la puissance du 0 face à toutes les fonctions. C'est toujours ça qui m'étonne. La fonction exponentielle tend vers + oo de plus en plus vite, mais la fonction 1/(1-x) tend encore plus vite vers +oo (asymptote) quand x tend vers 1 à gauche.
Autrement dit, il n'y a pas de fonction qui tend vers +oo plus vite que quand son dénominateur tend vers 0.

[Ben314]

Je suis pas sûr que ce soit vraiment la bonne façon de voir les choses :
- Déjà, lorsque tu as deux trucs qui tendent vers l'infini, mais pas pour les même x->???, je pense pas que ça ait bien du sens de se poser la question de savoir lequel des deux "tend le plus vite vers l'infini".
Tu pourrait me donner un vague début de définition traduisant le fait que "f(x) tend vers l'infini lorsque x->1 plus vite que g(x) ne tend vers l'infini lorsque x->oo" ?
Perso, je vois pas bien ce qu'on peut faire pour comparer...
- Ensuite, dans les deux cas (énoncé de départ et celui avec x²), on a . Or, pour une telle fonction, si on regarde, pour x fixé (a priori non nul) la limite lorsque y tend vers -x^2 de f(x,y), on a affaire à une fraction dont le dénominateur tend vers 0 et donc, si le numérateur ne tend pas vers 0, c'est à dire si g(x,-x²) est non nul (en supposant g continue) alors la fraction tend vers +oo.
Donc si g(x,-x²) n'est pas identiquement nul sur un voisinage de 0, on peut trouver des points (x,y) aussi proche que l'on veut de (0,0) tels que f(x,y) soit aussi grand qu'on veut ce qui, bien évidement est une obstruction majeure à la continuité de f en (0,0).
Et si je refait la preuve de façon un peu plus générale que les deux cas particulier déjà traités, c'est pour faire ressortir que la non continuité de f en (0,0) résulte uniquement du fait que si on a une fraction dont le dénominateur tend vers 0 et pas le numérateur, ça suffit à prouver que la fraction en question n'a pas de limite dans R.
Une autre façon de dire exactement la même chose, c'est que le dénominateur x^2+y, on n'a certes pas le droit de le prendre égal à zéro, mais on peut le faire tendre vers 0 à la vitesse qu'on veut en prenant des "trajet" de plus en plus près de la parabole y=-x^2 (on peut prendre y=-x^2+ où \alpha est une fonction quelconque donc qui peut tendre vers 0 aussi vite qu'on veut) alors que le numérateur, à moins qu'il ne soit lui aussi nul sur cette parabole, il va tendre vers 0 "à une certaine vitesse" et donc ne pourra pas rivaliser avec le dénominateur qu'on pourra toujours faire tendre vers 0 "plus vite que lui".

[zygomatique]

merci ben314 ça confirme l'idée de proximité que j'avais ... qui repose sur ce pb de diviser par 0 alors que le numérateur n'est pas nul ...

je je n'étais pas allé dans les détails comme toi et si j'ai écris un o(x^2) c'était dans l'idée qu'il fallait au moins une puissance de 2 ... qui n'est pas fausse mais en rentrant dans les détails on voit en fait que ça ne suffisait pas et qu'il fallait aller encore plus loin ...

l'idée était qu'on pouvait être aussi proche de la courbe x^2 + y = 0 ... tout le pb était de choisir cette bonne proximité !!!

[Ben314]

Si tu veut mon avis, de toute façon tout mon charabia est parfaitement résumé dans ton " y=-x^2+x^100 " où il me semble qu'on voit bien que le x^100 il est là pour dire "un truc qui tend vers 0 aussi vite que je veux"