Diverses problèmes rencontrés en Maths Spé.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 02 Sep 2015, 18:30
par PCTroyes » 02 Sep 2015, 18:30
Bonsoir ! Je mettrai ici tous les problèmes que je rencontre durant mon année de maths spé si jamais quelqu'un peut m'aider...
02/09/2015 : Trouver la limite de
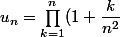)
03/09/2015 : Montrer que :
}=\frac{1}{n}-\frac{1}{n+1})
et
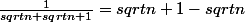
19/09/2015: f l'application de R²[X] dans R²[X] tel que :
+P( \frac{x+1}{2} )])
Question: Montrer que f est injective.
Merci de votre aide !
Je modifierai ce sujet régulièrement pour chaque problème rencontré.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Sep 2015, 18:35
par zygomatique » 02 Sep 2015, 18:35
salut
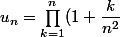 < (1 + \dfrac 1 n)^n)
en majorant k par n
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 02 Sep 2015, 18:44
par PCTroyes » 02 Sep 2015, 18:44
zygomatique a écrit:salut
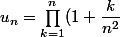 < (1 + \dfrac 1 n)^n)
en majorant k par n
....
Effectivement c'est un excellent majorant bravo et merci.
Ceci laisse place à la seconde partie du problème, étant donné qu'un majorant n'est pas forcément (souvent pas le cas d'ailleurs) la limite vers laquelle tant la fonction, comment trouver sa limite ?
Ps: merci beaucoup, auriez-vous lamabilité de me guider rapidement sur la façon de présenter les formules comme écrit à la main ?
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 02 Sep 2015, 18:52
par PCTroyes » 02 Sep 2015, 18:52
J'ai trouvé la limite, il était question d'utiliser une suite (Vn)-->1/2 quand n-->+INF
Avec Vn = ln(Un)
Donc Un-->Racine de EXP
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 03 Sep 2015, 18:53
par PCTroyes » 03 Sep 2015, 18:53
Nouveau bug sur cette petite égalité...
C'est sûrement débile et je m'en excuse mais bon...
}=\frac{1}{n}-\frac{1}{n+1})
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 03 Sep 2015, 19:16
par Sylviel » 03 Sep 2015, 19:16
part de la droite en mettant tout au meme denominateur...
Une petite egalite a avoir en tete, surtout en spe
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 03 Sep 2015, 19:28
par PCTroyes » 03 Sep 2015, 19:28
Merci Sylviel ! Je la note tout comme
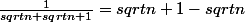
j'imagine


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Sep 2015, 19:39
par zygomatique » 03 Sep 2015, 19:39
petite remarque ::
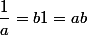
!!
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 03 Sep 2015, 19:44
par PCTroyes » 03 Sep 2015, 19:44
Merci beaucoup ! J'ai simplement l'impression de passer pour un imbécile mais je continuerai de poser mes questions...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Sep 2015, 19:51
par zygomatique » 03 Sep 2015, 19:51
t'inquiètes pas ... mieux vaut passer pour un imbécile auprès d'un con ... que le contraire .... :ptdr:
plus sérieusement : il vaut mieux poser des questions et avoir les réponses ....
mais cela ne doit pas te dispenser de penser et réfléchir aux réponses ... et ne pas oublier ses cours de collège (calcul algébrique et littéral ... avec les fractions, les puissances, les racines carrées ...)
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 04 Sep 2015, 08:39
par Pythales » 04 Sep 2015, 08:39
PCTroyes a écrit:J'ai trouvé la limite, il était question d'utiliser une suite (Vn)-->1/2 quand n-->+INF
Avec Vn = ln(Un)
Donc Un-->Racine de EXP
Petite remarque amicale : je suis étonné que tu aies trouvé la limite de

(elle est exacte), et que tu butes sur des égalités aussi simples que la décomposition de fractions ou des identités remarquables ...
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 04 Sep 2015, 15:39
par PCTroyes » 04 Sep 2015, 15:39
Pythales a écrit:Petite remarque amicale : je suis étonné que tu aies trouvé la limite de

(elle est exacte), et que tu butes sur des égalités aussi simples que la décomposition de fractions ou des identités remarquables ...
C'est toute ma particularité depuis un bon moment en maths, je m'en sors mieux dans ce qui peut paraître complexe, ce qui fait que des choses très simples me font buter...
Mon professeur m'avait dit que je pouvais tenter centrale à condition de corriger cela en étant plus rigoureux
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 04 Sep 2015, 15:54
par PCTroyes » 04 Sep 2015, 15:54
\leq x)
et
= \bigsum_{k=1}^{n} (1+ \frac{k}{n^2}))
Après on identifie x comme k/n^2 puis calcul de limites. J'ai fais comme ça.
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 19 Sep 2015, 15:19
par PCTroyes » 19 Sep 2015, 15:19
f l'application de R²[X] dans R²[X] tel que :
+P( \frac{x+1}{2} )])
Question 1: Ecrire la matrice de f dans la base B = (1,X,X²)
J'ai surtout besoin d'explications claires car j'ai du mal à visualiser les f(1),f(x) et f(x²) afin d'établir une matrice..
Je sais la faire cependant j'aimerai que l'on m'explique les nuances entres les X
Ex: Est-ce que f(X) = 0.5*(0.5X+0.5*(X+1)), f(1)=0.5*[1+1], si oui, pourquoi ?
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 19 Sep 2015, 16:54
par PCTroyes » 19 Sep 2015, 16:54
C'est réglé.
f l'application de R²[X] dans R²[X] tel que :
+P( \frac{x+1}{2} )])
Question: Montrer que f est injective.
Note: j'ai une matrice de la base B de f

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 19 Sep 2015, 17:10
par chombier » 19 Sep 2015, 17:10
PCTroyes a écrit:19/09/2015: f l'application de R²[X] dans R²[X] tel que :
+P( \frac{x+1}{2} ) \right ])
Question: Montrer que f est injective.
Merci de votre aide !
Je modifierai ce sujet régulièrement pour chaque problème rencontré.
C'est une application linéaire, il "suffit" de montrer que son noyau est nul
D'ailleurs il aurait mieux valu noter f comme ceci :
+P \left ( \frac{X+1}{2} \right ) \right ])
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
en majorant k par n
(elle est exacte), et que tu butes sur des égalités aussi simples que la décomposition de fractions ou des identités remarquables ...