Démonstrations diverses ( Traitement du signal )
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
amk
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Mai 2005, 01:14
-
par amk » 19 Oct 2006, 16:55
Bjr,
Je cherche à démontrer les relations suivantes :
Soit la fct d'auto corrélation :
 = \int_ {-\infty}^{+\infty} x(t).x*(t-\tau) dt)
Je cherche à démontrer la relation :
1/
 = \Gamma*{xx}(-\tau)))
J'ai procedé à un changement de variable :
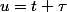
et j'obtiens :
 = \int_{-\infty}^{+\infty} x*(u).x(u-\tau) du)
Est ce bon ?
Je bloque pour la démonstration de :
2/ [tex]\left |\Gamma{xx}(\tau) \right | ment ( infiniment ^^ )
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
par jose_latino » 19 Oct 2006, 17:28
amk a écrit:Bjr,
Je cherche à démontrer les relations suivantes :
Soit la fonction d'auto corrélation :
 = \int_{-\infty}^{\infty} x(t)\overline{x(t-t_0)} dt)
Je cherche à démontrer la relation :
 = \overline{\Gamma_{xx}(t_0)})
J'ai procedé à un changement de variable : u = t+to et j'obtiens :
 = \int_{-\infty}^{\infty} x(u)\overline{x(u-t_0)} du)
Est ce bon ?
Tu n'as pas bien remplacé, c'est:
 = \int_{-\infty}^{\infty} x(u-t_0)\overline{x(u)} du)
Je bloque pour la démonstration de :
|\leq\Gamma_{xx}(0))
Utiliser l'inégalité de Cauchy-Schwarz pour les intégrales:
\left( \int |g|^2\right))
et pour :
|^2 \leq\Gamma_{xx}(0)\Gamma_{yy}(0))
j'ai utilisé la proprièté 2 pour la démontrer ( et encore j'ai parachuté un : Gamma_xy ment ( infiniment ^^ )
Encore l'inégalité de Cauchy-Schwarz. Bon courage! :zen:
-
amk
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Mai 2005, 01:14
-
par amk » 19 Oct 2006, 17:33
Pour la 1 en, effet :D tjs aussi tête en l'air :)
Pour la 2 et la 3 je vais essayer merci :)
-
amk
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Mai 2005, 01:14
-
par amk » 20 Oct 2006, 13:40
Aie je bloque sur la 2 malgré l'indication , pire je ne trouve aucune logique dans ce que je fais ,alors :
\right| = \int_{0}^{+\infty} |x(t)|dt)
donc ça n'aboutit à rien
Ou alors, j'ai mal utilisé cauchy , bref help me please
Merci bcp
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
par jose_latino » 20 Oct 2006, 13:49
Simplement, il faut remarquer que
\right|^2 dt=\int_{-\infty}^{+\infty}x(t).x*(t-0)dt)
et
\right|^2 dt=\int_{-\infty}^{+\infty} \left|x(t)\right|^2 dt)
:id:
-
amk
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Mai 2005, 01:14
-
par amk » 20 Oct 2006, 16:46
Ah oué fallait y penser
Merci beaucoup
Au fait , je bloque sur autre chose mnt , comment exprimer
)
en un produit de convolution ?
( PS : produit de convolution :
 = x(t)*y(t) = \int_{-\infty}^{+\infty}x(\tau).y(t-\tau) d\tau)
J'ai pensé à la dérivée car on peut trouver une relation entre
)
et
)
( faut mettre un - ) et j'ai essayé de faire ressortir le produit de convolution de la formule d'inter corrélation mais j'aboutis pas
. Est ce la bonne marche à suivre ?
Merci encore
-
panoramix
- Membre Relatif
- Messages: 108
- Enregistré le: 04 Sep 2006, 20:03
-
par panoramix » 20 Oct 2006, 22:13
Salut,
 = \int_{-\infty}^{+\infty} x(t).y*(t-\tau) dt)
On pose :
=x(\tau)*z(\tau))
avec
=y*(-t))
=\int_{-\infty}^{+\infty} x(t).z(\tau-t) dt)
donc
=\int_{-\infty}^{+\infty} x(t).y*(t-\tau) dt)
A+
-
amk
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Mai 2005, 01:14
-
par amk » 21 Oct 2006, 00:35
Merci beaucoup :)
-
amk
- Membre Naturel
- Messages: 21
- Enregistré le: 01 Mai 2005, 01:14
-
par amk » 27 Oct 2006, 12:55
jose_latino a écrit:Simplement, il faut remarquer que
:id:
Slt
Je veux juste revenir sur un point que j'ai trouvé étrange ?
Pourquoi cette égalité ? on a pris
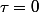
a t'on le droit ? car celà voudrait dire qu'il faut aussi remplacé le
du membre gauche de l'inégalité ?!
Merci
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
par jose_latino » 27 Oct 2006, 13:58
Non, tu peux arriver à la conclusion en faisant le changement de variables
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
par KIYU » 12 Mar 2017, 02:19
