Distributions: L2 et L1(loc)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
RadarX
- Membre Relatif
- Messages: 333
- Enregistré le: 24 Juil 2005, 19:39
-
 par RadarX » 26 Avr 2007, 22:31
par RadarX » 26 Avr 2007, 22:31
Bonsoir,
)
s'injecte dans
)
ou
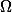
est un ouvert de
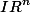
. On le prouve en montrant que l'application T:
)
--->
)
qui à
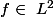
--->
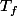
où
= \int\ _\Omega\ f.\phi\)
est lineaire injective et sequentiellement continue, cette derniere signifiant que si une suite
)
tend vers 0 dans

alors
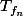
tend vers 0 aussi.
Mon bleme est de montrer la meme injection pour
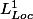
. Que signifierait alors qu'une suite
)
tende vers 0 dans
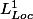
?
Merci.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 26 Avr 2007, 22:36
par tize » 26 Avr 2007, 22:36
Bonsoir,
RadarX a écrit:...alors T_{f_n} tend vers 0 aussi.
rafraichit moi la mémoire s'il te plait, c'est bien
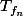
tend vers 0 en norme d'application linéaire ?
-
RadarX
- Membre Relatif
- Messages: 333
- Enregistré le: 24 Juil 2005, 19:39
-
 par RadarX » 27 Avr 2007, 13:50
par RadarX » 27 Avr 2007, 13:50
tize a écrit:Bonsoir,
rafraichit moi la mémoire s'il te plait, c'est bien
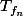
tend vers 0 en norme d'application linéaire ?
Non, ce n'est pas pour cette norme. De toute facon, je ne connais pas de norme pour l'espace
)
des distributions.
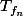
tend vers 0 signifie simplement que qq soit
)
,
= \int\ _\Omega\ {f_n}.\phi\)
tend vers 0 dans IR.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 27 Avr 2007, 14:13
par tize » 27 Avr 2007, 14:13
RadarX a écrit:...De toute facon, je ne connais pas de norme pour l'espace
)
des distributions...
Moi non plus, il n'en existe pas il me semble que c'est un espace topologique non normé.
En principe,
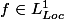
si la restriction de f à tout compact est intégrable je serai donc tenté de dire que
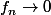
dans
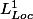
signifie que pour tout compact

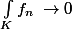
-
RadarX
- Membre Relatif
- Messages: 333
- Enregistré le: 24 Juil 2005, 19:39
-
 par RadarX » 27 Avr 2007, 15:04
par RadarX » 27 Avr 2007, 15:04
tize a écrit:En principe,
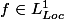
si la restriction de f à tout compact est intégrable je serai donc tenté de dire que
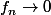
dans
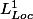
signifie que pour tout compact

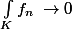
Cela parait logique (en tout cas naturel) de pencher pour cette définition. Reste à voir si cela a un sens!
Je suis surtout embeté de ne pas me souvenir avoir deja rencontré ce type de convergence. Enfin...
Merci Tize... et a tous.
-
Ted
- Membre Naturel
- Messages: 71
- Enregistré le: 26 Mar 2007, 21:22
-
 par Ted » 27 Avr 2007, 18:57
par Ted » 27 Avr 2007, 18:57
je crois que c'est plutot
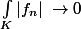
sinon je ne vois pas trop comment prouver quoi que ce soit...
-
oups01
- Membre Naturel
- Messages: 66
- Enregistré le: 27 Jan 2007, 14:08
-
 par oups01 » 27 Avr 2007, 19:50
par oups01 » 27 Avr 2007, 19:50
c assé simple
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
des distributions...
si la restriction de f à tout compact est intégrable je serai donc tenté de dire que
dans
signifie que pour tout compact
