quelqu'un peut m'aider pour trouver la derivée, au sens des distributions, de
Merci !
Au sens des distributions...
14 messages
- Page 1 sur 1
Au sens des distributions...
par Als128 » 02 Juin 2010, 19:44
Bonsoir,
quelqu'un peut m'aider pour trouver la derivée, au sens des distributions, de
car j'ai un peu de mal...
Merci !
quelqu'un peut m'aider pour trouver la derivée, au sens des distributions, de
Merci !
par MacManus » 02 Juin 2010, 20:17
Bonsoir.
il s'agit de|)\mathbb{1}_{[0,2 \pi]})
non ?
il faut revenir à la définition de la dérivation au sens des distributions.
Pour cela, on se donne une fonction "test"
de classe 
à support compact (ici 
). est donc nulle en dehors de ce compact.
il s'agit de
il faut revenir à la définition de la dérivation au sens des distributions.
Pour cela, on se donne une fonction "test"
par Als128 » 02 Juin 2010, 21:00
Oui, la parenthèse est passe à la trappe...
Pour le principe de départ, pas de problème, j'ai bien pris une fonction à support sur [0,2pi], en fait c'est le calcul ou je seche...
Je dois m'emmeler les pinceaux mais bon... j'y arrive pas
Pour le principe de départ, pas de problème, j'ai bien pris une fonction à support sur [0,2pi], en fait c'est le calcul ou je seche...
Je dois m'emmeler les pinceaux mais bon... j'y arrive pas
par MacManus » 02 Juin 2010, 21:25
il faut bien retenir que (au sens des distributions) 
, c'est à dire que
\phi(x)dx = -\Bigint_{-\pi}^{\pi}f(x)\phi'(x)dx)
, cad : |)'\phi(x)dx = -\Bigint_{-\pi}^{\pi}(1+|sin(x)|)\phi'(x)dx<br />= -\Bigint_{-\pi}^{0}(1+|sin(x)|)\phi'(x)dx - \Bigint_{0}^{\pi}(1+|sin(x)|)\phi'(x)dx)
...
tu vois comment continuer ?
tu vois comment continuer ?
par MacManus » 02 Juin 2010, 21:39
Bon je continue un peu : )
la dernière égalité est encore égale à :
-dx - \Bigint_{0}^{\pi}\phi'(x)dx -\Bigint_{-\pi}^{0}|sin(x)|\phi'(x)dx - \Bigint_{0}^{\pi}|sin(x)|\phi'(x)dx)
=dx + \Bigint_{-\pi}^{0}sin(x)\phi'(x)dx-\Bigint_{0}^{\pi}sin(x)\phi'(x)dx)
(d'après le signe du sinus sur 
et sur 
)
Or,dx=0)
car est à support compact sur 
. Ensuite, il ne te reste qu'à effectuer 2 IPP pour les 2 autres intégrales puis enfin et surtout à utiliser la définition de la dérivation au sens des distributions, pour "identifier" la dérivée de ta fonction.
la dernière égalité est encore égale à :
-
=
Or,
par MacManus » 02 Juin 2010, 22:21
Je m'aperçois que si on est un peu futé, on remarque que |)
est une fonction paire (et 
-périodique). Ce qui veut dire que
|)dx = 2\Bigint_{0}^{\pi}(1+|sin(x)|)dx)
.
Par définition de la dérivation au sens des distributions, on a, pour toute fonction testde classe à surpport compact, qui est l'intervalle, 
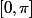
, cad :
|)'\phi(x)dx = -2\Bigint_{0}^{\pi}(1+|sin(x)|)\phi'(x)dx)
Donc, en divisant par 2 des deux côtés et en développant l'intégrale de droite, c'est encore égal à :
-dx - \Bigint_{0}^{\pi}|sin(x)|\phi'(x)dx)
Ordx = 0)
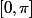
car est une fonction à support compact, donc s'annule en particulier aux bords (en 0 et en ). De plus, sur , la fonction sinus est positive, donc, l'égalité précédente est égale à :
-\phi'(x)dx = \Bigint_{0}^{\pi}cos(x)\phi(x)dx)
(si on effectue 1 IPP et si on utilise encore le fait que est à support compact).
Donc au final, on obtient :
|)'\phi(x)dx = \Bigint_{0}^{\pi}cos(x)\phi(x)dx)
On a donc montrer que la dérivée au sens des distributions de la fonctionest la fonction )
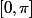
, pour tout x de .(par identification des intégrandes)
Par définition de la dérivation au sens des distributions, on a, pour toute fonction test
Donc, en divisant par 2 des deux côtés et en développant l'intégrale de droite, c'est encore égal à :
-
Or
-
Donc au final, on obtient :
On a donc montrer que la dérivée au sens des distributions de la fonction
par alavacommejetepousse » 03 Juin 2010, 03:50
bonjour cela ne va pas on ne peut pas se limiter à [0,pi] car phi est quelconque on doit couper l'intégrale en 2
par MacManus » 03 Juin 2010, 10:36
Oui tu as raison, j'avais d'ailleurs commencer par couper en deux l'intégrale, comme quoi la 1ére idée est toujours la meilleure. Donc pour ne pas perdre en généralité, j'ai suivi ton conseil et j'ai pour ma part (re)trouvé le résultat sur [0,2pi] cette fois. Je laisse cependant Als128 chercher! Le principe est le même que dans mon post précédent.
par vingtdieux » 03 Juin 2010, 21:59
Cette fonction malgré la valeur absolue est continue. Donc la dérivée est la même qu'au sens classique. C'est cette dérivée qui est discontinue au point pi. Donc c'est sur la dérivee seconde qu'intervient les diracs.
par Doraki » 04 Juin 2010, 08:43
f est discontinue en 0 et en 2pi, donc il y a des diracs en ces deux points.
par vingtdieux » 04 Juin 2010, 09:42
Où sont les points de discontinuités de la fonction ?
A la limite si on avait 1 ailleurs de l'intervalle 0 a 2 Pi.... Mais l'énoncé n'est pas clair à ce niveau là. On aurait alors:
delta(x)-delta(x-2Pi) + g(x)
Avec g(x) la fonction cos(x) de 0 à Pi et -cos(x) de Pi à 2Pi
A la limite si on avait 1 ailleurs de l'intervalle 0 a 2 Pi.... Mais l'énoncé n'est pas clair à ce niveau là. On aurait alors:
delta(x)-delta(x-2Pi) + g(x)
Avec g(x) la fonction cos(x) de 0 à Pi et -cos(x) de Pi à 2Pi
par vingtdieux » 04 Juin 2010, 14:19
Alors c'est la solution que j'ai avancée. Il y a un saut positif en 0 et un saut négatif en 2 Pi. La fonction se derive par ailleurs en enlevant la valeur absolue suivant le domaine de la variable.
Ca veut bien dire que l'on a alors une distribution, telle quelle la ligne n'a pas de sens, il faut l'utiliser dans un calcul de < >.
Ca veut bien dire que l'on a alors une distribution, telle quelle la ligne n'a pas de sens, il faut l'utiliser dans un calcul de < >.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :