Distance a un sous-espace vectoriel

[Maths-ForumR]

Bonjour,
Voici un exercice sur lequel je bloque :

ERREUR D'AFFICHAGE #

###############################################################
##############################################################
#############################################################

[Ben314]

Salut,

Déterminer inf Intégrale (de 0 à 1) (√t -(at+b))^2

De deux choses l'une : soit il manque un carré dans l'intégrale (et il y en a un de trop sur le b) que tu doit minimiser, soit... tout ce que tu as fait n'a rien a voir avec la question... (et j'en profite pour te suggérer plus que fortement de te mettre au MimeTeX si tu veut qu'on comprenne ce que tu écrit).

Sinon, en supposant que c'est la première hypothèse qui est la bonne, le début de ton laïus est correct, mais tes et , c'est n'importe quoi : vu le point de vue qu'on a, , ne désigne pas un vecteur de ton espace, mais un scalaire donc ton truc a autant de sens que si tu écrivait que tu fait le produit scalaire d'un vecteur de R² avec un réel...

EDIT : en plus, dans ta prose, il désigne deux trucs qui n'ont rien à voir (ou presque) l'un avec l'autre : au début, c'est un réel à déterminer (dans l'intégrale) et plus loin tu utilise la même lettre pour désigner la norme de

[Maths-ForumR]

Oui vous avez raison pardon !

Mais je ne vois pas quel systeme résoudre

[Ben314]

Si désigne la fonction et le projeté orthogonal de sur le plan vectoriel engendré par les fonction et on doit évidement avoir avec 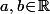mais aussi orthogonal à tout vecteur du plan, c'est à dire orthogonal à et à .
Donc ...

[Maths-ForumR]

Donc (f-g|uo)=0 et (f-g|u1)=0 mais c'est ça que je n'arrive pas a résoudre

[Ben314]

Rappel : et là dedans, tu connait absolument tout, sauf les réels et .

[Maths-ForumR]

donc f-g=√t-a+x ?

[Ben314]

donc f-g=√t-a+x ?

"plus ou moins" on va dire...
Ecrit tel quel, ça n'a pas de sens vu qu'à gauche du = tu as une fonction et à droite un réel (et qu'en plus ton "réel" il est pas terrible).
Donc
- Soit tu écrit le truc en terme de fonction : (à gauche et à droite du = c'est des fonctions)
- Soit tu l'écrit en terme de réels : , (à gauche et à droite du = c'est des réels)
(évidement, si tu préfère, tu peut écrire que , )

C'est évidement toujours important de faire la différence entre fonction et réel, mais c'est encore plus le cas dans ce type d'exo où les fonctions jouent le rôle de vecteur et les réels celui de scalaire : c'est vraiment absurde d'écrire (est-ce qu'au Lycée tu aurais écrit qu'un vecteur de R² était égal à 5 ?)

Perso, j'ai tendance à écrire le plus longtemps possible les trucs en terme de fonction vu que c'est plus court, mais ça oblige à donner des noms à toute les fonction qu'on manipule, par exemple ici, ça oblige à donner un nom aux fonctions et . Mais ça permet de bien mieux faire la différence entre les "vecteurs" et les "scalaires".

P.S. Par rapport a l'énoncé de départ, j'ai échangé les rôles de et (lorsque j'ai écrit que )

[Maths-ForumR]

Je ne vois pas comment calculer le profuit scalaire v:
(f-g |uo)=0

[Ben314]

.

Or ; et

[Maths-ForumR]

(uo|uo)=1
(u1|uo)= 1+x²
(f|uo)=x +1

et pour l'autre calcul :

(u1|u1)=1
(f|u1)=x²+x

[Ben314]

(uo|uo)=1
(u1|uo)= 1+x²
(f|uo)=x +1

(u1|u1)=1
(f|u1)=x²+x

A part la première (uo|uo), le reste est faux.
En particulier, vu que u1, u0 et f sont des fonctions parfaitement définies et ne dépendant pas du tout d'un quelconque paramètre, je ne comprend pas bien comment tu fait pour trouver des produits scalaires dépendant d'un paramètre x.
Est-ce que, si je te donne deux vecteurs U et V tout ce qu'il y a de plus fixes dans R², ça te semble plausible que le produit scalaire de U avec V soit égal à 1+x² ?

Et pour (u1|u1), là tu as pas mis de x, mais... c'est faux quand même : (u1|u1)=1/3

[Maths-ForumR]

Je ne vois pas comment vous obtenez (u1|u1)=1/3

[Ben314]

Avec... la définition que tu as donné pour le produit scalaire...

[Maths-ForumR]

Ha merci
Donc (u1|uo)= 1/2 ; (h|uo)= 2/3 ; (h|u1) = 2/5 ?

[Ben314]

Oui.
Il te reste à calculer (f|u0) et (f|u1) puis a résoudre le système linéaire

[Maths-ForumR]

(h|uo)= 2/3 ; (h|u1) = 2/5 ?

Et je trouve a= -12/5 et b = 28/5

Donc p(h)= (-12/5).t - 28/5 avec mes notation car notre a et b sont inversés

Mais il me reste une étape c'est bien ça je dois trouver un nombre a la fin
il faut que je calcul : ||h-p(h)||² ? Je ne sais pas trop quoi faire

[Ben314]

Ton résultat semble... très déraisonnable...
Je te rappelle qu'en fait, on cherche le segment de droite qui, en un certain sens, approxime le mieux la courbe de t->racine(t) sur [0,1].
Or j'ai pas vraiment l'impression que t-> (-12/5).t - 28/5 soit une "bonne approximation" de t->racine(t) (trace la courbe de t->racine(t) et ta droite sous géogébra si vraiment tu voit pas le problème...)

Perso, j'ai la même chose que toi pour (u0|h) et (u1|h), mais après résolution du système, j'obtiens p(t)=4/5.t+4/15 qui, graphiquement parlant, semble bien plus raisonnable comme approximation de t->racine(t).

Après, une fois que tu auras le bon a et le bon b, pour trouver la distance, on peut essayer des trucs subtils, mais on peut aussi très bêtement écrire que et calculer l'intégrale.

[Maths-ForumR]

Je suis un peu perdu car nos notation sont inversées
Moi j'ai : avec p(h)=aU0+bU1 et U0->t , U1->1
(uo|uo)=1
(u1|uo)= 1/2
(f|uo)= 2/5
(u1|u1)= 1/3
(f|u1)=2/3

D’où le système :
a+(1/2)b=2/5
(1/2)a+(1/3)b=2/3

Pour obtenir la même chose que vous je dois inverser le 2/3 et le 2/5 dans le systeme mais pourquoi ?

[Ben314]

Je suis un peu perdu car nos notation sont inversées

Oui, j'ai a peu prés tout écrit "à l'envers" par rapport aux notations de départ de l'exercice, désolé.

Moi j'ai : avec p(h)=aU0+bU1 et U0->t , U1->1
(uo|uo)=1
(u1|uo)= 1/2
(f|uo)= 2/5
(u1|u1)= 1/3
(f|u1)=2/3

Si tu prend U0:t->t et U1:t->1 alors tout tes (Un|Um) sont "à échanger", par exemple (U0|U0)=1/3
Sauf que c'était très con de ma part de pas prendre la même chose que l'énoncé pour le et le , mais que pour les fonctions Un, ça semble quand même plus logique de prendre Un:t->t^n.

P.S. Et essaye de prendre la (bonne) habitude d'écrire "U0:t->1" ou bien "pour tout t dans ??? U0(t)=1" et pas d'autres trucs comme U0->t qui risque de te faire faire des erreurs (confondre des "vecteurs" et des "scalaires").
A mon sens, le fait qu'en math on ait des notations assez strictes, c'est des fois un peu chiant, mais ça permet d'éviter pas mal d'erreur consistant à écrire des truc absurdes du style vecteur+scalaire. Par exemple ici, ça peut paraitre "pédant" de distinguer le réel 1 et la fonction constante égale à 1, mais c'est pour pas se mélanger les pinceaux...