Distance et projecteur orthogonaux
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 30 Aoû 2017, 12:48
par mehdi-128 » 30 Aoû 2017, 12:48
Bonjour,
E est un R espace vectoriel de dimension finie supérieure ou égal à 1. E est muni du produit scalaire <.> ce qui lui confère une structure d'espace euclidien.
Soit n un vecteur non nul de E et H l'hyperplan de E orthogonal à n :
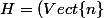^{\perp})
Exprimer pour

la distance
)
en fonction de

et

Comme H est un sous espace vectoriel de E alors :
=||x-p_H (x)||)
et là je bloque.
Merci.
-
FLBP
- Habitué(e)
- Messages: 289
- Enregistré le: 25 Aoû 2017, 01:07
-
 par FLBP » 30 Aoû 2017, 12:57
par FLBP » 30 Aoû 2017, 12:57
Normalement ça devrait donner :
 = \frac {|<x,n>|}{||n||})
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 30 Aoû 2017, 13:24
par mehdi-128 » 30 Aoû 2017, 13:24
Je vois pas comment obtenir ça.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 30 Aoû 2017, 13:47
par Pseuda » 30 Aoû 2017, 13:47
Bonjour,
Le théorème de Pythagore avec un point quelconque de H ? La projection orthogonale réalise la distance minimum à l'hyperplan.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 30 Aoû 2017, 14:09
par mehdi-128 » 30 Aoû 2017, 14:09
En utilisant :
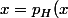 + p_{H^{\perp}})
}=\frac{<x,n>}{||n||^2}n)
Donc :
=\frac{||<x,n>||}{||n||})
Juste une question pourquoi on a :

?
-
FLBP
- Habitué(e)
- Messages: 289
- Enregistré le: 25 Aoû 2017, 01:07
-
 par FLBP » 30 Aoû 2017, 14:15
par FLBP » 30 Aoû 2017, 14:15
c'est

, simplement la valeur absolue du produit scalaire, pour obtenir une distance toujours positive.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 30 Aoû 2017, 14:25
par mehdi-128 » 30 Aoû 2017, 14:25
Oui je vois mais comment on montre que :

Car le produit scalaire est un réel ?
Car je suis parti de la formule de la distance avec la norme.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 30 Aoû 2017, 14:34
par Pseuda » 30 Aoû 2017, 14:34
Pour moi,

ne veut rien dire, puisque c'est un réel. Dans une étape du calcul, c'est

.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 30 Aoû 2017, 14:57
par arnaud32 » 30 Aoû 2017, 14:57

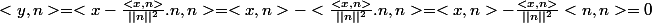
donc y est dans H
pour tout z de H,


or y-z est dans H (car c'est un ev)
donc
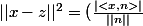^2+||y-z||^2)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 30 Aoû 2017, 15:40
par mehdi-128 » 30 Aoû 2017, 15:40
Pseuda a écrit:Pour moi,

ne veut rien dire, puisque c'est un réel. Dans une étape du calcul, c'est

.
Bah :
=||x-p_H (x)||=||\frac{<x,n>}{||n||^2} n||)
Par linéarité du produit scalaire ;
=\frac{1}{||n||^2} ||<x,y>n||=\frac{1}{||n||^2} ||n|| \times |<x,y>|)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
