[Niv. SUP] DM de maths : Projecteur et espace vectoriel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Déc 2007, 15:08
par zelda007 » 30 Déc 2007, 15:08
Bonjour à tous,
Je bloque sur un MD de maths :
Soit p un endomorphisme de E tel que p o p = p
1) Soit y appartenant à E. Montrer que : y appartient à Im(p) y = p(y)
Le sens je bloque. Je sais que si y appartient à Im(p) alors il existe un x appartenant à E tel que y = p(y) mais après que faire ?
Merci :we:
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 30 Déc 2007, 15:13
par trust » 30 Déc 2007, 15:13
Il existe

t.q.
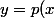 = p(p(x)) = p(y))
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Déc 2007, 15:16
par Nightmare » 30 Déc 2007, 15:16
Salut !
Soit y dans Im(p), il existe x tel que p(x)=y
On a alors pop(x)=p(y) soit p(x)=p(y)
d'où par transitivité y=p(y)
:happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Déc 2007, 15:17
par Nightmare » 30 Déc 2007, 15:17
En retard, désolé.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Déc 2007, 15:18
par zelda007 » 30 Déc 2007, 15:18
Lol c'était tout bête !! :ptdr:
On me demande maintenant de montrer que Im(p) = Ker(Ide - p) et que Ker(p) et Im(p) sont en somme directe (donc montrer que Ker(p) "inter" Im(p) = {Ide}).
PS : Si y'a une possibilité de faire les symboles de mathsn je suis prenneur (je connais pas le LATEX) :)
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 30 Déc 2007, 15:21
par trust » 30 Déc 2007, 15:21
t'as pas un livre d'algèbre linéaire tout prêt de toi? parce que c'est un exercice typique qui se trouve facilment dans les livres...
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Déc 2007, 15:23
par zelda007 » 30 Déc 2007, 15:23
Ah bon ? Non désolé je n'ai pas de bouquin... mais sur le net j'ai rien trouvé mais je m'y suis sans doute mal pris. De toute manière les réponses m'interesse pas, c'est la démarche qui compte et le but est que je comprenne.
Donc si vous pouviez me guider :D
Merci
-
rafbh
- Membre Relatif
- Messages: 250
- Enregistré le: 19 Nov 2006, 17:07
-
 par rafbh » 30 Déc 2007, 15:25
par rafbh » 30 Déc 2007, 15:25
Avec y dans imp il existe x dans E tq y=p(x)
é puis tu calcule y-p(y)=p(x)-pop(x)=0 car pop=pd'ou imp inclus ker(ide-p)
avex x dans ker(ide-p) on a x-p(x)=0 on obtient x=p(x) dou x appar imp
ainsi ker(---) inclus imp
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 30 Déc 2007, 15:26
par trust » 30 Déc 2007, 15:26
essaie la double inclusion ...
-
rafbh
- Membre Relatif
- Messages: 250
- Enregistré le: 19 Nov 2006, 17:07
-
 par rafbh » 30 Déc 2007, 15:27
par rafbh » 30 Déc 2007, 15:27
jte laisse la somme directe fastoche
mais demande si tu coince!!
n'hésites surtout pas meme si les remarques de certains sont découragentes!!
Mais il sont sympa t'inquiétes
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Déc 2007, 15:38
par zelda007 » 30 Déc 2007, 15:38
rafbh a écrit:jte laisse la somme directe fastoche
mais demande si tu coince!!
n'hésites surtout pas meme si les remarques de certains sont découragentes!!
Mais il sont sympa t'inquiétes
Merci pour vos aides. En tout cas c'est rapide !! et c'est très rare sur un forum :we:
Je viens de comprendre ta démo, juste une précision dans cet exo, Ide c'est bien la fonction nulle ou alors c'est la fonction qui à x ===> x ?
Pour la somme directe, le problème c'est que on a jamais vu ce que c'était. On a juste une ligne disans que : si F et G sont en sommes directes alors F inter G = {l'élément neutre}. Mais vu que je n'ai jamais vu ce genre de démo, je ne sais pas par où commencer... :briques:
-
rafbh
- Membre Relatif
- Messages: 250
- Enregistré le: 19 Nov 2006, 17:07
-
 par rafbh » 30 Déc 2007, 15:49
par rafbh » 30 Déc 2007, 15:49
x>>>>x
tu prends y dans imp inter kerp
il existe x dans E tq y=p(x) or p(y)=0 cr y dans kerp dou pop(x)=p(x)=0 or y=p(x)
on obtient bien y=0.
N'hésites surtout pas!!
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Déc 2007, 16:03
par zelda007 » 30 Déc 2007, 16:03
C'est tellement simple que j'ai l'impression d'être un abruti !
Tu n'a pas répondu mais d'après toutes les démos, tu me confirmes bien que Ide dans ce exo c'est bien l'application nulle ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 30 Déc 2007, 16:05
par Joker62 » 30 Déc 2007, 16:05
Ide c'est l'identité
Qui à un vecteur x associe le même vecteur x :)
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 30 Déc 2007, 16:06
par trust » 30 Déc 2007, 16:06
non, je ne crois pas....
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Déc 2007, 16:13
par zelda007 » 30 Déc 2007, 16:13
Certes mais Ide c'est l'élément neutre dans cet exo donc c'est pas la fonction nulle ? car si c'est l'application qui a x associe x alors les démos de rafbh sont fausses :
tu prends y dans imp inter kerp
il existe x dans E tq y=p(x) or p(y)=0 cr y dans kerp dou pop(x)=p(x)=0 or y=p(x)
on obtient bien y=0.
Dans ces démos, il y a des "0" partout...
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 30 Déc 2007, 16:16
par trust » 30 Déc 2007, 16:16
t'as des 0 partout parce que tu es dans le noyau...
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Déc 2007, 16:22
par zelda007 » 30 Déc 2007, 16:22
La définition du noyau :
x appartient à Ker(f) f(x) = {l'élément neutre} et dans cet exo l'élément neutre est : Ide donc il y a quelque chose que je ne comprends pas. Ca doit etre les vacances qui m'abrutisse.
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 30 Déc 2007, 16:27
par trust » 30 Déc 2007, 16:27
dans le cas ici, p(x) est un point, pas une application. Si je crois bien, E est un espace vectoriel, l'élement neutre est donc 0.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Déc 2007, 16:33
par zelda007 » 30 Déc 2007, 16:33
trust a écrit:dans le cas ici, p(x) est un point, pas une application. Si je crois bien, E est une espace vectoriel, l'élement neutre est donc 0.
p est un endomorphisme de E et E est une ev donc effectivement l'élément neutre est 0. C'est moi qui m'embrouille les pinceaux...
Donc maintenant, on pose q = Ide - p. Trouver q o q et montrer que Im(Ide - p= Ker(p).
q o q = (Ide - p) o (Ide - p), y'a des propriétés connues sur "o" ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
