Matrice d'un projecteur

[Maths-ForumR]

que P=Im(p)=ker(ide-p)

[Robot]

Non. Ces propriétés sont vérifiées,, mais ça ne caractérise pas la projection sur P parallèlement à D. La preuve, on ne voit pas D dans ce que tu écris.

[Maths-ForumR]

Je ne sais pas alors

[Robot]

Relis ton cours. Un exercice qui accompagne un cours utilise des notions définies dans le cours.

[Maths-ForumR]

Dans mon cours il n'y a que les propriétés admises !
Peut on dire p est la projection sur P parallélement à D signifie que p(x)=xP ?

[Robot]

Dans mon cours il n'y a que les propriétés admises !
Peut on dire p est la projection sur P parallélement à D signifie que p(x)=xP ?

Que veut dire xP ??

Dans ton cours sur les supplémentaires, il y a sans doute écrit quelconque chose de ce genre.
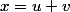
Soient et des sous-espaces supplémentaires de . Alors tout élément de se décompose de manière unique sous la forme avec et ; l'application linéaire s'appelle la projection sur parallèlement à . Autrement dit, la projection sur parallèlement à est l'application linéaire telle que pour tout et pour tout .

[Maths-ForumR]

Je ne vois toujours pas comment écrire p(z) et p(a)..

[Robot]

Je ne vois toujours pas comment écrire p(z) et p(a)..

C'est que tu ne lis pas ce que j'écris :

"La projection sur parallèlement à est l'application linéaire telle que pour tout et pour tout ."

[Maths-ForumR]

Donc si j'ai compris :
f(y)=(1,0,0)
f(z)=(0,0,0)
f(a)=(0,0,0) ?

[Robot]

Non, tu n'as pas vraiment compris.
Première chose, il vaut mieux ne pas changer de notation. On a noté la projection sur parallèlement à , ne te mets pas à la noter maintenant.
Ensuite, appartient à , donc par définition de on a . Or n'est pas le vecteur de . Ce qu'on a c'est que les coordonnées de dans la base sont : . Si tu mélanges les deux, tu seras irrémédiablement perdu.

[Maths-ForumR]

Donc
p(y)=y car y appartient à P
P(z)=z car z appartient à P
P(a)=0 car a appartient à D ?

[Robot]

Ca c'est correct. Maintenant il te reste à écrire la matrice de p dans la base (y,z,a), puis à appliquer le changement de base pour avoir la matrice de p dans la base canonique.
(Ce n'est peut-être pas la méthode la plus aisée pour arriver à la matrice de p dans la base canonique).