Bonjour,
J'ai montré en cours qu'un projecteur est toujours diagonalisable. Mais une partie de la démonstration que nous avons faite me chiffonne, je vous l'écris en espérant que vous puissiez éclaircir mes idées....
p est un projecteur, on a donc p²=p c'est à dire p²-p=0
Soit Q(x)=x²-x=x(x-1)
Q est un polynôme annulateur de p, donc le polynôme minimal (noté m) de p divise le polynôme annulateur de p.
Voici ma question: Peut on dire que m=x, ou m=x-1 ou m=x(x-1)? Ou est ce que m vaut obligatoirement x(x-1)?
La démonstration se termine en disant que le polynôme minimal est scindé à racines simples, donc p est diagonalisable.
Merci pour votre aide!!
Montrer qu'un projecteur est diagonalisable
10 messages
- Page 1 sur 1
Monsieur23 a écrit:Aloha,
Prend par exemple le projecteur sur {0}, et le projecteur sur E tout entier. Quels sont leurs polynômes minimaux ?
J'essaie de comprendre... Pour le projecteur sur {0}, on peut dire que dim(Im(p))=0. Or en notant A la matrice de p, je sais que Im(p) est engendré par les vecteurs colonnes de A.
Tout vecteur est envoyé sur le vecteur nul, donc A serait la matrice nulle?
Dans ce cas l'unique valeur propre de A serait 0, donc le polynôme minimal vaudrait x?
MC91 a écrit:J'essaie de comprendre... Pour le projecteur sur {0}, on peut dire que dim(Im(p))=0. Or en notant A la matrice de p, je sais que Im(p) est engendré par les vecteurs colonnes de A.
Tout vecteur est envoyé sur le vecteur nul, donc A serait la matrice nulle?
Dans ce cas l'unique valeur propre de A serait 0, donc le polynôme minimal vaudrait x?
Plus simplement, le projecteur sur {0}, c'est la fonction nulle (la matrice nulle), donc son polynôme minimal, c'est x.
Et le projecteur sur l'espace tout entier ?
« Je ne suis pas un numéro, je suis un homme libre ! »
MC91 a écrit:La fonction identité?
Dans ce cas, le polynôme caractéristique vaut (1-X)², et le polynôme minimal vaut (1-X)?
Salut. Oui puisque l'identité donne une matrice diagonale!!! ( tout comme la matrice nulle) donc tu peux avoir m=x, m=x-1 ou m=x(x-1) comme on te l'a signalé. Dans tous les cas, ce sont des polynômes scindés à racines simples. D' où le résultat.
( c'est à vérifier, je dis peut-être n'importe quoi)
jlb a écrit:Salut. Oui puisque l'identité donne une matrice diagonale!!! ( tout comme la matrice nulle) donc tu peux avoir m=x, m=x-1 ou m=x(x-1) comme on te l'a signalé. Dans tous les cas, ce sont des polynômes scindés à racines simples. D' où le résultat.
( c'est à vérifier, je dis peut-être n'importe quoi)
D'accord, merci beaucoup pour cette réponse! :we:
Bonjour,
Pas tout à fait :
*le polynôme caractéristique est (X-1)^n -ou bien (1-X)^n, selon ta définition- où n est la dimension de E.
*le polynôme minimal est X-1, et non 1-X, car il est par définition unitaire.
Sinon, par définition du projecteur sur F parallèlement à G, on a :
*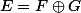
*pour tout x de F, p(x)=x
*pour tout x dans G, p(x)=0
On voit facilement que F est l'espace propre associé à 1 et G l'espace propre associé à 0.
Ces deux espaces propres étant supplémentaires, p est diagonalisable.
MC91 a écrit:La fonction identité?
Dans ce cas, le polynôme caractéristique vaut (1-X)², et le polynôme minimal vaut (1-X)?
Pas tout à fait :
*le polynôme caractéristique est (X-1)^n -ou bien (1-X)^n, selon ta définition- où n est la dimension de E.
*le polynôme minimal est X-1, et non 1-X, car il est par définition unitaire.
Sinon, par définition du projecteur sur F parallèlement à G, on a :
*
*pour tout x de F, p(x)=x
*pour tout x dans G, p(x)=0
On voit facilement que F est l'espace propre associé à 1 et G l'espace propre associé à 0.
Ces deux espaces propres étant supplémentaires, p est diagonalisable.
emdro a écrit:Bonjour,
Pas tout à fait :
*le polynôme caractéristique est (X-1)^n -ou bien (1-X)^n, selon ta définition- où n est la dimension de E.
*le polynôme minimal est X-1, et non 1-X, car il est par définition unitaire.
Sinon, par définition du projecteur sur F parallèlement à G, on a :
*
*pour tout x de F, p(x)=x
*pour tout x dans G, p(x)=0
On voit facilement que F est l'espace propre associé à 1 et G l'espace propre associé à 0.
Ces deux espaces propres étant supplémentaires, p est diagonalisable.
Merci pour cette réponse
Oui désolé, je me plaçais dans R².
Ok pour le polynôme minimal, j'avais oublié qu'il devait être unitaire.
La remarque d'après est très intéressante, je n'y avais jamais pensé! On trouve directement les deux valeurs propres d'un projecteur en fait, et ses sous espaces propres!
Par contre je ne comprends pas cette phrase : Ces deux espaces propres étant supplémentaires, p est diagonalisable.
Peut être que c'est du à une propriété que j'ai oublié...
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
