Dimension d'un sous espace propre.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 02 Jan 2016, 20:19
par PCTroyes » 02 Jan 2016, 20:19
Bonsoir,
Soit un entier n>=2, z1 et z2 deux complexes tels que z2

0.
M la matrice : M= Où retrouver l'article avec les formules TEX ?
Donc M= Une matrice carré avec z1 sur la diagonale et tous les autres termes égaux à z2
Montrer que M admet un s-e propre de dimension n-1.
J'ai essayé de calculer le polynôme caractéristique comme une brute ce qui est horrible.
Ce qui est absurde étant donné la dimension n..
J'ai appliqué la formule du polynôme caractéristique pour n=2 : X^2 - 2z1X + z1^2
Et le montrer par récurrence mais je ne m'en sors pas..
Des conseils ?
Merci
-
Robot
 par Robot » 02 Jan 2016, 20:31
par Robot » 02 Jan 2016, 20:31

est une valeur propre de

si et seulement si
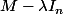
est de rang
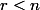
. Le sous-espace propre associé à

est le noyau de
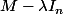
, il est de dimension

(théorème du rang).
Chercher un sous-espace propre de dimension

revient donc à chercher

tel que
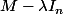
soit de rang 1.
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 02 Jan 2016, 23:01
par PCTroyes » 02 Jan 2016, 23:01
Merci Robot. J'ai deux questions, je remercie d'avance quiconque me répondra.
1) "Chercher un sous-espace propre de dimension

revient donc à chercher

tel que
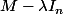
soit de rang 1."
Cela n'est-il pas vrai ssi il existe deux valeurs propres ? Si oui, comment le montrer ?
2) Un peu en dehors du problème c'est plus pour ma culture: "

est une valeur propre de

si et seulement si
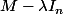
est de rang
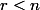
. "
Que se passe t'il alors si r=n ?
Merci.
Note, nous avons tendance à travailler avec
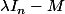
au lieu de
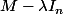
depuis une réforme il me semble, cela change t-il quelque chose ?
-
Robot
 par Robot » 02 Jan 2016, 23:26
par Robot » 02 Jan 2016, 23:26
PCTroyes a écrit:1) "Chercher un sous-espace propre de dimension

revient donc à chercher

tel que
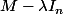
soit de rang 1."
Cela n'est-il pas vrai ssi il existe deux valeurs propres ? Si oui, comment le montrer ?
Non, pas "si". Il est nécessaire qu'il y ait deux valeurs propres exactement (tu vois pourquoi ?), mais ce n'est pas suffisant !
PCTroyes a écrit:2) Un peu en dehors du problème c'est plus pour ma culture: "

est une valeur propre de

si et seulement si
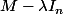
est de rang
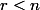
. "
Que se passe t'il alors si r=n ?
Ben,
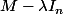
est inversible et

n'est pas valeur propre. What else ?
PCTroyes a écrit:Note, nous avons tendance à travailler avec
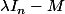
au lieu de
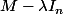
depuis une réforme il me semble, cela change t-il quelque chose ?
Je suis d'accord pour que le polynôme caractéristique soit
)
. Mais pour parler du rang,
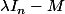
ou
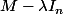
, c'est kif-kif.
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 02 Jan 2016, 23:53
par PCTroyes » 02 Jan 2016, 23:53
Robot a écrit:Non, pas "si". Il est nécessaire qu'il y ait deux valeurs propres exactement (tu vois pourquoi ?), mais ce n'est pas suffisant ! .
Il faut bel et bien deux valeurs propres exactement afin de retomber sur des dimensions 1 et n-1. Je vois pourquoi, je ne saurai répondre autrement qu'en disant qu'il faut que la somme des dimensions de ces sous espaces propre = n M est diagonalisable, je m'écarte alors du sujet non ?
Merci pour les deux autres réponses Robot !
Quel lien il y a t'il entre l'inversibilité de la matrice M-Lambda In et le fait que lambda ne soit pas valeur propre ?
-
Robot
 par Robot » 03 Jan 2016, 08:05
par Robot » 03 Jan 2016, 08:05
Je ne suis pas sûr que tu aies une vision claire de ce que veulent dire "condition nécessaire" et "condition suffisante". En écrivant qu'il y a un sous-espace propre de dimension n-1 si et seulement s'il y a exactement deux valeurs propres, tu affirmes que c'est une condition nécessaire et suffisante. Tu te trompes, c'est juste une condition nécessaire.
"Quel lien il y a t'il entre l'inversibilité de la matrice M-Lambda In et le fait que lambda ne soit pas valeur propre ?"
Le lien est simple : il s'agit de deux propriétés équivalentes.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Jan 2016, 09:44
par zygomatique » 03 Jan 2016, 09:44
salut
un exemple simple :: soit (e_1,e_2, ..., e_n) une base et f l'endomorphisme défini par ::
f(e_i) = e_i) lorsque i < n et f(e_n) = e_1
f admet un sous-espace propre de dimension n - 1 ... et qu'une seule valeur propre ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Robot
 par Robot » 03 Jan 2016, 09:54
par Robot » 03 Jan 2016, 09:54
Zygomatique, dans ton exemple il y a deux valeurs propres : 1 et 0.
Mais tu as tout de même raison dans le fait qu'un endomorphisme peut avoir un sous-espace propre de dimension n-1 et une seule valeur propre : modifier ton exemple avec
=0)
pour
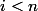
.
Je corrige donc mon affirmation en une qui est correcte (et triviale) : un endomorphisme diagonalisable qui a un sous-espace propre de dimension n-1 a nécessairement deux valeurs propres.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Jan 2016, 10:23
par zygomatique » 03 Jan 2016, 10:23
ha oui .... merci ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 03 Jan 2016, 13:00
par Pseuda » 03 Jan 2016, 13:00
PCTroyes a écrit:Quel lien il y a t'il entre l'inversibilité de la matrice M-Lambda In et le fait que lambda ne soit pas valeur propre ?
La matrice M-;)In est inversible si et seulement si dét(M-;)In);)0 ssi

n'est pas solution du polynôme caractéristique de M ssi

n'est pas valeur propre de M.
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 03 Jan 2016, 13:16
par PCTroyes » 03 Jan 2016, 13:16
Merci j'arrive mieux à le voir dès à présent.
Pour en revenir à mon exercice.
J'essaye alors de trouver un

tel que
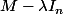
soit de rang 1.
J'ai naturellement essayé avec
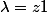
pour obtenir une diagonale de 0 ce qui ne sert pas à grand chose car je ne trouve pas de famille liée de taille 1...
-
Robot
 par Robot » 03 Jan 2016, 14:17
par Robot » 03 Jan 2016, 14:17
Rang 1 veut dire que la matrice n'est pas nulle et que toutes les colonnes (ou toutes les lignes) appartiennent à la même droite vectorielle.
Tu peux choisir facilement

pour que toutes les colonnes de
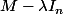
soient en fait égales.
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 03 Jan 2016, 14:32
par PCTroyes » 03 Jan 2016, 14:32
Ce que je dois chercher : un Lambda tel que la matrice M-Lambda In possède une ligne (colonne) étant combinaison linéaire de toutes les autres.
Effectivement si elles sont égales c'est réglé.
Mais pour la matrice M possédant z1 sur la diagonale et tous les autres termes égaux à z2, je ne dois pas avoir la même facilité que vous pour trouver un lambda Robot... A mon grand désespoir...
-
Robot
 par Robot » 03 Jan 2016, 14:38
par Robot » 03 Jan 2016, 14:38
PCTroyes a écrit:Ce que je dois chercher : un Lambda tel que la matrice M-Lambda In possède une ligne (colonne) étant combinaison linéaire de toutes les autres.
Ce n'est absolument pas ce que j'ai écrit !!!! Là, ce que tu écris, ça veut juste dire que M-Lambda In est de rang plus petit que n.
PCTroyes a écrit: Effectivement si elles sont égales c'est réglé.
Mais pour la matrice M possédant z1 sur la diagonale et tous les autres termes égaux à z2, je ne dois pas avoir la même facilité que vous pour trouver un lambda Robot... A mon grand désespoir...
M'enfin ??? chaque colonne a toutes ses coordonnées égales à
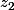
, sauf la coordonnée correspondant à son numéro qui est
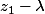
. Franchement, pas besoin d'être un génie pour trouver

tel que toutes les colonnes soient égales (elles devront être égales à quoi ?)
-
PCTroyes
- Membre Naturel
- Messages: 70
- Enregistré le: 01 Sep 2015, 17:51
-
 par PCTroyes » 03 Jan 2016, 14:49
par PCTroyes » 03 Jan 2016, 14:49
Désolé si je vous ai agacé mais j'ai tout compris maintenant et je vous remercie infiniment grâce à ce dernier message !
Effectivement si une ligne ou colonne est combinaison linéaire des autre cela signifie que le rang est inférieur à n et non pas égal à 1 je le vois bien maintenant et je me rend compte de mon ânerie.
Ensuite il est clair qu'il faut que z1-Lambda = z2 d'où Lambda = z1 - z2.
J'ai honte mais bon j'ai compris c'est l'essentiel !
Encore une fois merci pour tout Robot, votre patience et vos explications aussi claires que possible pour un forum.
Sans doutes à bientôt !
-
Robot
 par Robot » 03 Jan 2016, 14:52
par Robot » 03 Jan 2016, 14:52
Quand on a compris, on se demande comment on a fait pour ne pas comprendre avant.
Bon courage !
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 03 Jan 2016, 15:25
par Pseuda » 03 Jan 2016, 15:25
Tu peux aussi calculer le polynôme caractéristique de M : (z1-z2-;))^(n-1) * (z1+(n-1)z2--;)) (par combinaison linéaire des lignes), en déduire ses 2 valeurs propres et ses 2 sous-espaces propres.
-
Robot
 par Robot » 03 Jan 2016, 16:18
par Robot » 03 Jan 2016, 16:18
Oui, pourquoi faire simple quand on peut faire compliqué ? :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
