Differentiel et gradient
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 04 Juil 2007, 13:19
par Babe » 04 Juil 2007, 13:19
Bonjour,
voila en physique en utilise tres frequemment les deux formules qui suivent (differentiel et gradient). C'est bien d'aplliquer sans savoir lol :zen: mais j'aimerais savoir quand meme d'où elle vienne.
merci d'avance
 \mathrm df = \frac{\partial f}{\partial x_1} \mathrm dx_1 <br /> + \frac{\partial f}{\partial x_2} \mathrm dx_2 + ... + \frac{\partial f}{\partial x_n} \mathrm dx_n)
 df= \vec{grad}(f(M)).d\vec{M})
il me semble logique que la 2e decoule de la 1er (quoique ...ce qui semble logique l'est pas toujours)
par contre c'est surtout la 1er qui m'interpelle
-
Riemann
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2007, 13:43
-
 par Riemann » 04 Juil 2007, 16:00
par Riemann » 04 Juil 2007, 16:00
La première égalité est la forme développée du produit scalaire grad(f(M)).dM.
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 04 Juil 2007, 16:06
par Babe » 04 Juil 2007, 16:06
oui je suis d'accord les 2 formules veulent dire la mm chose
mais d'ou provient
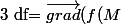).d\vec{M})
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 04 Juil 2007, 17:10
par B_J » 04 Juil 2007, 17:10
Salut;
si tu as x=y
et z=y alors x=z non ?
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 04 Juil 2007, 17:15
par Babe » 04 Juil 2007, 17:15
oui je suis d'accord que les deux formules sont equivalentes mais j'aimerais savoir d'ou vienne ces formules.
elles ont bien une origine mathematique
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 04 Juil 2007, 17:17
par B_J » 04 Juil 2007, 17:17
que vaut gard(f(M)) ? que vaut dM ? et grad(f(M)).dM ?
conclusion ?
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 04 Juil 2007, 17:50
par Babe » 04 Juil 2007, 17:50
je sais que grad f(M) vaut
)
et que
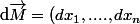)
et que en appliquant le produit scalaire on obtient 1)
mais la question est pourquoi df est egal a cela
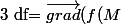).d\vec{M})
il y a bien une raison c'est pas un iluminé qui a ecrit cela pour s'amuser
 par Dominique Lefebvre » 04 Juil 2007, 18:15
par Dominique Lefebvre » 04 Juil 2007, 18:15
Babe a écrit:je sais que grad f(M) vaut

et que

et que en appliquant le produit scalaire on obtient 1)
mais la question est pourquoi df est egal a cela

il y a bien une raison c'est pas un iluminé qui a ecrit cela pour s'amuser
Physiquement, cette équation exprime le fait que le champ de vecteurs
grad(f) est orthogonal aux surfaces de niveau (f(M) = Cte).
PS : on peut aussi rappeler la propriété importante du gradient que veut que la circulation élémentaire du gradient d'une fonction f soit égale à la différentielle de cette fonction...
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 04 Juil 2007, 18:23
par Joker62 » 04 Juil 2007, 18:23
B_J a écrit:Salut;
si tu as x=y
et z=y alors x=z non ?
La relation = est transitive dans tout les ensembles ?
Edit : En même temps elle est définie comme Relation d'équivalence, donc bon c'était une question sans sens.
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 04 Juil 2007, 19:05
par Babe » 04 Juil 2007, 19:05
merci dominique
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 05 Juil 2007, 00:16
par quinto » 05 Juil 2007, 00:16
Pourquoi on a ça ?
C'est tout simplement par définition de la différentielle.
-
easyprepa
- Messages: 3
- Enregistré le: 04 Juil 2007, 11:12
-
 par easyprepa » 05 Juil 2007, 12:23
par easyprepa » 05 Juil 2007, 12:23
il y a sur le site easyprepa tout un document sur le gradient, différentielle,... à télécharger.
http://www.easyprepa.fr.tcpage d'accueil > sup > cours mpsi > en bas de la page se trouve ce que tu cherches.
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 05 Juil 2007, 13:22
par Babe » 05 Juil 2007, 13:22
merci easyprepa tout s'illumine :id:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités



