Cryptocatron-11 a écrit:Bonsoir,
Voici un exercice dont j'ai la correction mais que je comprend pas trop j'ai souligné ce qui me perturbe
On a

On pose
=\int_{0}^{x} e^{\frac{t^2}{2}} dt)
Donc
=e^{\frac{x^2}{2}})
On a donc
=e^{\frac{-x^2}{2}} g(x))
= u'v + v'u = e^{\frac{-x^2}{2}} g'(x) + \frac{-2x}{2} e^{\frac{-x^2}{2}} g(x)= e^{\frac{-x^2}{2}} (g'(x)-x g(x)) = \frac{e^{\frac{x^2}{2}}}{e^{\frac{x^2}{2}}} - \frac{x \times g(x)}{e^{\frac{x^2}{2}}}= 1- x f(x))
car
=\frac{g(x)}{e^{\frac{x^2}{2}}})
On a donc une équation différentielle de la forme y'+xy=1
avec y(0)=0 je ne comprends pas pourquoi y(0)=0
Après on nous demande de calculer le DSE à savoir
=\sum_{0}^{\infty} a_n x^{2n+1})
qui est une fonction impair
je ne comprends pas non plus pourquoi f est impair !Ensuite on trouve
 = \sum_{0}^{\infty} (2n+1)a_n x^{2n})
facilement en dérivant
=\sum_{0}^{\infty} a_n x^{2n+1})
on doit trouver f'(x)+xf(x)=1
+xf(x)= \sum_{0}^{\infty} (2n+1)a_n x^{2n} +a_n x^{2n+2} = a_0 + \sum_{0}^{\infty} ((2n+1)a_n + a_{n-1}) x^{2n} = 1)
Et ma grande question (on y arrive enfin ! )
Il trouve
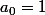
Mais j'ai vraiment pas du tout compris pourquoi

Et du coup ça nous permet de déduire que
a_n + a_{n-1})=0)
et trouver

mais je suis bloqué pour savoir d'ou sort le
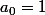
Un grand merci pour votre aide

Salut Cryptocatron-11
Résumons :
On a une fonction f(x) qui est définie par une intégrale.
Première propriété de f(x) :
Pour x=0, l'intégrale est nulle (puisque ses deux bornes sont égales). Donc f(0)=0.
Autre propriété :
D'une part, exp(-x²/2) est paire. D'autre part, l'intégrale est impaire car la fonction intégrée exp(x²/2) est paire. f(x) , qui est le produit de exp(-x²/2) par l'intégrale, est donc impaire.
Des calculs préliminaires démontrent que f(x) est une solution d'une équation différentielle :
y'+xy=1
Parmi toutes les solutions y(x) de cette équa.diff. la solution y(x)=f(x) a la particularité d'être telle que y(0)=f(0)=0 comme on vient de le voir.
Ensuite f(x) est mis sous forme de série, qui est la somme d'un premier terme constant et d'autres termes qui sont des puissances de x. Pour x=0, tous ces autres termes sont nuls. Il ne reste que le terme constant. Et il est donc nul puisqu'on sait que, pour x=0, la somme est nulle : f(0)=0.
