Dans toute la suite :
Soient :
On pose :
Quelle est l'équation differentielle qui met en lien
Un exemple qui ressemble un peu à celà, pour vous comprenez de quoi je parle :
Soit
Alors
On a :
c'est-à-dire
et, compte-tenu de
Merci d'avance ! :happy3:
Serie entière et équation differentielle
13 messages
- Page 1 sur 1
Serie entière et équation differentielle
par barbu23 » 02 Jan 2010, 18:58
Bonsoir à tous : :happy3:
Dans toute la suite :
étant un entier fixe.
Soient :
:
On pose :
:
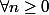
Quelle est l'équation differentielle qui met en lien
, 
et probablement d'autres } $)
avec 
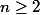
telle que :
 = \displaystyle \sum_{n \geq 0} u_{n} \frac{x^{n}}{n!} $$)
Un exemple qui ressemble un peu à celà, pour vous comprenez de quoi je parle :
Soit une serie entière definie par :  = 1 + x^2 + \displaystyle \sum_{n \geq 2} 2^2.4^2\ldots(2n-2)^2 \frac{x^{2n}}{(2n)!}\) $)
.
Alors = 2x + \displaystyle \sum_{n \geq 2} a_{2n-1} x^{2n-1}\) $)
avec ^2}{(2n-1)!}\) $)
On a :a_{2n+1} = 2na_{2n-1} $)
, donc, pour tout élément  $)
:
a_{2n+1}x^{2n} = \displaystyle \sum_{n\geq2} 2na_{2n-1} x^{2n} = x^2 \displaystyle \sum_{n\geq2} (2n-1)a_{2n-1} x^{2n-2} + x \displaystyle \sum_{n\geq2} a_{2n-1} x^{2n-1},\] $)
c'est-à-dire
 - 2 - 3a_3x^2 = x^2[f''(x)-2] + x[f'(x)-2x] $)
et, compte-tenu de
est solution sur 
de l'équation différentielle
y' - xy = 2(1 - x^2).$)
Merci d'avance ! :happy3:
Dans toute la suite :
Soient :
On pose :
Quelle est l'équation differentielle qui met en lien
Un exemple qui ressemble un peu à celà, pour vous comprenez de quoi je parle :
Soit
Alors
On a :
c'est-à-dire
et, compte-tenu de
Merci d'avance ! :happy3:
par wserdx » 02 Jan 2010, 22:29
Étudie le cas 
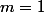
. Tu devrais facilement identifier la fonction 
associée grâce son développement en série entière, et en déduire dans le cas général.
par fatal_error » 02 Jan 2010, 22:39
salut,
si on prend juste le terme
Et qu'on remplace on a
 = \bigsum_{k = 0} \frac{(a_1x)^k}{k!}\\)
On dérive, on a
 = a_1 \bigsum_{k = 1} \frac{(a_1)^{k-1}}{(k-1)!}\\<br />g'(x) = a_1 \bigsum_{k = 0} \frac{(a_1)^{k}}{k!}\\<br />g'(x) = a_1g(x))
avec g(x) c'est quasi comme f(x)
si on prend juste le terme
Et qu'on remplace on a
On dérive, on a
avec g(x) c'est quasi comme f(x)
la vie est une fête 
par barbu23 » 03 Jan 2010, 14:06
Oui ;  = \displaystyle \sum_{i=1}^{m} e^{a_{i} x} $)
, mais c'est pas ça ce qui m'interesse mais, mais moi je cherche l'équation differentielle qui regitces fonctions ! :happy3:
Merci d'avance !
Merci d'avance !
par greg78 » 03 Jan 2010, 14:26
On peut toujours essayer la solution bourrine. Tu dérives et tu cherches si une relation apparaît entre les dérivées successives.
par barbu23 » 03 Jan 2010, 14:28
Oui, j'ai bien testé cette methode, mais je n'ai pas aboutit à grande chose malheureursmeent ! :happy3: et en fait, c'est cette methode bourrine qui m'interesse ! :hum: :ptdr:
par fatal_error » 03 Jan 2010, 14:37
salut,
déjà on peut magouiller.
Si t'as identifié
 = e^{a_ix})
Tu peux déjà dire que
 = a_i f(x))
Bon, maintenant si on suppose qu'on connait pas le developpement en serie de la forme exponentielle (!!!)
on a
 = \bigsum_{k=0} \frac{(a_ix)^k}{k!})
On dérive terme a terme
 = a_i \bigsum_{k=1} \frac{(a_ix)^{k-1}}{(k-1)!})
Le k=1 vient du fait du terme constant qui gicle et qui n'a plus lieu d'etre
 = a_i \bigsum_{k=0} \frac{(a_ix)^k}{k!} = a_i f(x))
Il faut préciser pourquoi est-ce qu'on a le droit de dire que la somme de la serie qu'on dérive c'est a egal a la somme de chacun des termes dérivés de la série
déjà on peut magouiller.
Si t'as identifié
Tu peux déjà dire que
Bon, maintenant si on suppose qu'on connait pas le developpement en serie de la forme exponentielle (!!!)
on a
On dérive terme a terme
Le k=1 vient du fait du terme constant qui gicle et qui n'a plus lieu d'etre
Il faut préciser pourquoi est-ce qu'on a le droit de dire que la somme de la serie qu'on dérive c'est a egal a la somme de chacun des termes dérivés de la série
la vie est une fête
par barbu23 » 03 Jan 2010, 15:37
et donc :
Par contre, fatal_error, quelle est le but derrière ton idée ? :happy3:
Merci d'avance ! :happy3:
par wserdx » 03 Jan 2010, 16:05
En supposant que les 
soient distincts deux à deux, tu dois pouvoir montrer que la famille des fonctions 
forme un espace vectoriel de dimension m.
La fonction et toutes ses dérivées appartiennent à cet espace, tu dois pouvoir monter que la famille })
forme une base,
et que},f^{(m)})
est une famille liée, et donc il existe une relation linéaire }=0)
Tu devrais voir apparaitre une matrice de Vandermonde de)
(à vue de nez...)
La fonction
et que
Tu devrais voir apparaitre une matrice de Vandermonde de
(à vue de nez...)
par barbu23 » 03 Jan 2010, 16:08
Ohhh mère ! je ne comprends absolument rien ! :king:
Svp ! un peu plus de details pour me mettre sur la voix ! je suis complètement perdu ! :hum:
Merci d'avance ! :happy3:
Svp ! un peu plus de details pour me mettre sur la voix ! je suis complètement perdu ! :hum:
Merci d'avance ! :happy3:
par wserdx » 03 Jan 2010, 17:22
En effet pour faire plus simple, tu peux voir qu'on peut écrire une relation matricielle:
}) = (e^{a_1x},\ldots,e^{a_mx}) M)
.
La matrice est une matrice dite de Vandermonde associée à la famille
, et qui est inversible si les sont distincts deux à deux.
En écrivant})
par un changement de base :
} = (e^{a_1x},\ldots,e^{a_mx})(a_1^m,\ldots,a_m^m)^t)
} = (f,f',\ldots,f^{(m-1)})M^{-1}(a_1^m,\ldots,a_m^m)^t)
Les coefficients de l'équation différentielle que tu cherches sont donc
^t)
La matrice est une matrice dite de Vandermonde associée à la famille
En écrivant
Les coefficients de l'équation différentielle que tu cherches sont donc
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :