Déterminer élasticités partielles

[antoine73]

Bonjour (ou bonsoir) :lol3:
Mon exo est le suivant: Déterminer les élasticités partielles de la fonction f définie sur (R*+)² par f(x,y) = e^(x/y).

Très honnêtement j'ignore totalement ce que je dois faire mon cours me parait incompréhensible.
J'ai fait les dérivé partielle première suivante : ;)f/;)x(x,y) = (1/y)*e^(x/1), ;)f/;)y(x,y) = (-x/y)e^(1/y)

dérivée 2nd : ;)'f/;)x(x,y)= (1/y)*(1/y)*e^(x/y), ;)'f/;)x;)y(x,y)= -1/y + e^(x/y) + 1/y

Je sais pas trop si ça va me servir.

Du coup j'aimerai bien que quelqu'un me montre comment il ferai ça et qu'il me l'explique avec des mots d'enfant vu que j'aurai d'autres question comme ça en TD :ptdr:

Merci d'avance!

[mrif]

Si tu connais l'élasticité d'une fonction à une variable, pour obtenir l'élasticité d'une fonction de 2 variables par rapport à l'une de ses variables (x ou y), on se ramène à une fonction d'une variable en considérant l'autre comme une constante.

Dans ton exo tu calcules l'élasticité des fonctions:
et
y est une constante dans l'expression de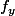 , et x est une constante dans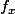

Pour info, tes calculs de dérivées partielles comortent des erreurs.