Bonsoir a tous, je dois calculer la d²f(0)(h,h) d'une fonction deux fois différentiable de E dans F (des espaces de Banach) sachant que pour tout t dans R, f(tx)=t²f(x)
En fait je dois montrer que d²f(0)(h,h) = 2f(h) :
Je pensais utiliser les dérivées directionnelles mais je suis bloqué, je ne vois pas comment procéder, si quelqu'un à un plan, je suis preneur.
Merci bien, cordialement.
Dérivées directionnelles, différentielle seconde
7 messages
- Page 1 sur 1
Ben, ici, ton "o(1)" il est pas super clair : un o(1) ça veut dire un truc qui tend vers 0 quand la variable tend vers 0, sauf que la variable, on voit pas trop qui c'est ici...
Normalement, si tu as fait les calculs comme je les aurais fait, ton "o(1)", en fait il tend vers 0 lorsque t tend vers 0 (le t que tu as du introduire au dessus) et, normalement, tu as déja fait tendre le t vers 0 au dessus d'où, ton "o(1)"... il vaut 0.
Normalement, si tu as fait les calculs comme je les aurais fait, ton "o(1)", en fait il tend vers 0 lorsque t tend vers 0 (le t que tu as du introduire au dessus) et, normalement, tu as déja fait tendre le t vers 0 au dessus d'où, ton "o(1)"... il vaut 0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
lorsque j'écris la formule de taylor à l'ordre 2 en O j'obtiens
f(h)=df(0)(h)+1/2 d²f(0)(h,h)+||h||²o(1) c'est la formule que j'a dans mon cours.
Puis je l'applique en th j'obtiens
f(th+h)=f((t+1)h)=(t+1)df(0)(h)+1/2(t+1)²d²f(0)(h,h)+(t+1)²||h||²o(1)
puis je fais tendre t->0 mais mon o(1) ne disparait pas ?!
merci de votre aide
cordialement
f(h)=df(0)(h)+1/2 d²f(0)(h,h)+||h||²o(1) c'est la formule que j'a dans mon cours.
Puis je l'applique en th j'obtiens
f(th+h)=f((t+1)h)=(t+1)df(0)(h)+1/2(t+1)²d²f(0)(h,h)+(t+1)²||h||²o(1)
puis je fais tendre t->0 mais mon o(1) ne disparait pas ?!
merci de votre aide
cordialement
Oui, mais l'incovéniant de la notation o(1) que tu emploie ici, c'est qu'on ne voit pas bien de quoi ça dépend : dans la "formule du cours", c'est clair, ça dépend de h, mais lorsque tu remplace par "t fois h"...
Je te donne "ma prose" (quasi identique sauf pour le o(1)) :
=f(0)+d_f(0)(h)+\frac{1}{2}d^2_f(0)(h,h)+||h||^2\varepsilon(h))
où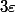 est une fonction de
est une fonction de  dans
dans  qui tend vers
qui tend vers 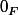 en
en 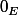 .
.
Si on fixe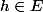 , alors, pour tout
, alors, pour tout  , on a :
, on a :
=f(th)=f(0)+d_f(0)(th)+\frac{1}{2}d^2_f(0)(th,th)+||th||^2\varepsilon(t h)<br />=f(0)+t\,d_f(0)(h)+\frac{t^2}{2}d^2_f(0)(h,h)+t^2||h||^2\varepsilon(t h))
Si tu fait tendre vers 0, tu en déduit que
vers 0, tu en déduit que 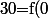)
Puis, si tu divise par et que tu fait tendre
et que tu fait tendre  vers 0, tu en déduit que
vers 0, tu en déduit que 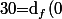(h))
Puis, si tu divise par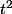 et que tu fait tendre
et que tu fait tendre  vers 0, tu en déduit que
vers 0, tu en déduit que =\frac{1}{2}d^2_f(0)(h,h))
Car, lorsque vers 0,
vers 0,  tend vers
tend vers 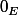 donc
donc ) vers
vers 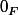
En résumé, si tu veut rédiger avec du "o(1)", il faut comprendre que le "o(1)" de la formule du cours tend vers 0 lorsque h->0. Donc, quand tu remplace h par t.h, le "nouveau" o(1) tend vers 0 lorsque t.h->0, donc, pour h fixé, il tend vers 0 lorsque t->0.
Je te donne "ma prose" (quasi identique sauf pour le o(1)) :
où
Si on fixe
Si tu fait tendre
Puis, si tu divise par
Puis, si tu divise par
Car, lorsque
En résumé, si tu veut rédiger avec du "o(1)", il faut comprendre que le "o(1)" de la formule du cours tend vers 0 lorsque h->0. Donc, quand tu remplace h par t.h, le "nouveau" o(1) tend vers 0 lorsque t.h->0, donc, pour h fixé, il tend vers 0 lorsque t->0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
