Dérivée de ln ∘ ln ∘ ⋯ ∘ ln

[Tekso]

Bonjour,
Je suis en classe préparatoire et je vous demande votre aide sur un exercice sur les dérivées successives : Dérivée de
ln ∘ ln∘ ⋯∘ln (n compositions avec n ∈ℕ).
J’ai essayé de dérivée plusieurs fois:
(Ln(x))’ = 1/x
(Ln(ln(x)))’ = 1/x*ln(x)
(Ln(ln(ln(x))))’ = 1/x*ln(x)*ln(ln(x))
(Ln(ln(ln(ln(x)))))’ = 1/x*ln(x)*ln(ln(x))*ln(ln(ln(x)))

On vois bien que 1/x est toujours présent et que à chaque dérivée il y’a un ln(x) qui se rajoute (1/x * 1/ln(x) * 1/ln(ln(x)) * …).
Mais je n’arrive pas a trouvé le terme général de la dérivée.
(Il faudra sûrement aussi utiliser de la récurrence quelque part mais aucune idée de comment et ou)
Merci de votre aide

[GaBuZoMeu]

Bonsoir,

Tes formules ne sont pas parenthésées correctement : 1/x*ln(x) est . Ce n'est pas ce que tu voulais écrire.

Ensuite, tu sais certainement que . C'est tout ce qu'il faut pour ta récurrence.

[Tekso]

Oui tout à fait je voulais plutôt écrire
1/(x*ln(x)*ln(ln(x) … ), mais je ne vois pas en quoi
la dérivée de ln(u)’ m’aidera pour trouver un terme général
a ln round ln round … rond ln

[GaBuZoMeu]

Même si ?

[Tekso]

J’ai essayé de réfléchir avec votre aide, mais je n’arrive pas à avoir l’idée

[GaBuZoMeu]

Pas d'idée à avoir, ça marche tout seul pour la récurrence.
On peut utiliser une notation pour faciliter l'écriture : on définit la suite de fonction par et (la fonction est le logarithme népérien itéré fois). De la sorte, on a la relation de récurrence .

[Pisigma]

Bonjour,

voir ici https://forums.futura-sciences.com/mathematiques-superieur/920440-derivee-de-ln-ln-ln.html

sympa pour les aidants!!

[tournesol]

On a les conventions pour écrire cela:
pour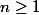 , on a
Avec les conventions et

[GaBuZoMeu]

Pourquoi ? Ça marche aussi pour .

[tournesol]

Effectivement et avec mes conventions . Quelle cécité!
Le paradoxe c'est que la lumière vienne du diable qui est en toi : celui qui se cache dans les détails ...

[Tekso]

Ok merci beaucoup je vais le reprendre du début et essayer de dénicher mes petites faiblesses, merci encore