Derivée n°ienne

[bienvenu200x]

Derivée n°ieme de la fonction f(x)=

Code: Tout sélectionner

exponentiel(xracine3)sinusx

[girdav]

Formule de Leibniz?

[bienvenu200x]

Merci , en faite je n'arrive pas à l'appliqué sur cette fonction .

[busard_des_roseaux]

Derivée n°ieme de la fonction f(x)=

Code: Tout sélectionner

exponentiel(xracine3)sinusx

Bj,



f(x) est la partie imaginaire d'une exponentielle. Et ça marche car

f(x)=u(x)+iv(x)
f'(x)=u'(x)+iv'(x)

mézaussi




pour

[girdav]

On a et la modération risque de me taper sur les doigts si je donne et .

[bienvenu200x]

si je prend f(x)=sinx et g(x)=exponentiel(x;)3)

[girdav]

Voilà. Maintenant il te faut calculer les dérivées d'ordre de chacune de ces fonctions.

[bienvenu200x]

Ockay . par exemple avec la fonction f(x)=(x²+1)e^x , avec k =3 on s'arrête et on fait la somme . Mais avec cette fonction le k n' est pas délimité et on nous demande de démontré que f(x);) =2;)e^(;)3) sin;)(x+n;);)6)

[girdav]

Puisque l'on te donne la formule tu peux tenter une preuve par récurrence.

[bienvenu200x]

Ockay je vais essayé

[busard_des_roseaux]

Bj,



Lemme 1
si alors (1)
que l'on réécrit

La dérivation par rapport à la variable réelle commute avec
la partie imaginaire

Lemme 2
La dérivée n-ième de est avec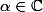


calcul

on transforme f en la partie imaginaire d'une fonction de dans



on dérive n fois


s'exprime agréablement sous forme trigo


conclusion