Densité de Q et minoration
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 03 Avr 2019, 17:08
par guillaume100 » 03 Avr 2019, 17:08
Bonjour,
Je seche sur un exo où il faut montrer qu'il existe C appartenant à R tel que pour tout entier relatif p et tout en tier naturel non nul q :
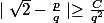
J'ai utilise la densite mais ca marche pas mais je pense que c'est un tout autre moyen parce que je cherche a montrer une minoration. Quelqu'un a une indication svp ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Avr 2019, 17:40
par Doraki » 03 Avr 2019, 17:40
En quelque sorte on te demande de montrer une version effective de l'irrationalité de sqrt(2) (puisque pour tout rationnel tu obtiendrais un minorant non trivial de la distance entre le rationnel et sqrt(2))
Tu pourrais commencer par regarder ta preuve favorite de l'irrationnalité de 2 et voir si tu peux en tirer une minoration non triviale de quelquechose.
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 03 Avr 2019, 18:02
par guillaume100 » 03 Avr 2019, 18:02
Merci pour la reponse j'ai montrer que racine de 2 est irrationnel en disant que s'il etait rationnel il existe des nombres premiers entre eux p et q tels que leur quotient fasse racine de 2, et en mettant au carre j'arrive au resultat
Ainsi je peux ecrire que racine de 2 c'est un toujours un rationnel plus epsilon, et la je bloque
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Avr 2019, 18:42
par Doraki » 03 Avr 2019, 18:42
Donc tu as montré que si p,q sont 2 entiers premiers entre eux alors p² <> 2q² ?
Donc que p² - 2q² est non nul.
Mais avoir une inégalité en > 0 ou en >= 0, comme tu le vois ce n'est pas suffisant, il faut faire mieux.
Peux-tu trouver un minorant de |p² -2q²| qui soit strictement positif et qui soit indépendant de p ou de q (du moment qu'ils ne soient pas nuls tous les deux) ?
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 03 Avr 2019, 18:52
par guillaume100 » 03 Avr 2019, 18:52
Merci beaucouo j'ai trouvé
p et q sont des entiers, donc p^2-2q^2 est un entier non nul, non nul de surcroît.
Alors p^2-2q^2 est superieur en valeur absolu à 1
Maitenant j'obtient preque l'inegalite avec cela mais j'ai le 2 au carré et pas de racine de 2, a partir de la on fait quoi svp ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Avr 2019, 18:59
par Doraki » 03 Avr 2019, 18:59
Oui, il est au moins >= 1, et ça, ça va être utile.
Maintenant, si tu regardes plus en détail comme tu passes de "sqrt(2) = p/q" à "p² = 2q²", tu devrais sentir
que c'est presque la même chose (mais ça ne l'est pas à cause d'une étape que tu as fait dans la preuve d'irrationalité, qu'il serait bon d'identifier)
Pour avoir la relation précise entre les deux ça serait utile de trouver une expression E telle que
(p - q sqrt(2)) * E = p²-2q²
parceque ça c'est bien la version algébrique de "si p = q * sqrt 2 alors p²-2q² = 0".
Une fois que tu as trouvé E tu auras donc |p-q sqrt(2)| >= 1 / |E| et tu pourras continuer
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 03 Avr 2019, 20:05
par guillaume100 » 03 Avr 2019, 20:05
Ah ouais j'ai compris merci !
E c'est egal à p+sqrt(2)
De là j'obtiens p-qsqrt(2) superieur ou egal à 1/(p+q*sqrt(2)) que je minore par 1/q en valeur absolu, et en divisant l'inegalite par q on obtient le resultat avec C=1
Edit: en fait je peux pas minorer par 1/q, mais ma minoration depend de p et q, et je vois pas comment enlever p
Par contre je vois pas quelle etape de la demo de l'irrationnalite peut servir
-
aviateur
 par aviateur » 03 Avr 2019, 21:16
par aviateur » 03 Avr 2019, 21:16
Bonjour
Je crois que les indications t'ont été données mais tu n'arrives pas à les exploiter.
posons
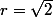
et
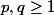
deux entiers quelconques.
^2|=q^2|2 -p^2/q^2|=|2 q^2-p^2|\in \N^*)
(déjà vu et tout est là) donc
^2|\geq 1)
ou encore
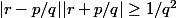
(1).
Supposons que |r-p/q|<1. donc i.e |r+p/q|=r+p/q<2r+1 et
(1) implique
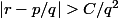
avec C=1/(2r+1).
Supposons que
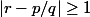
alors
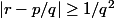

-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 04 Avr 2019, 19:59
par guillaume100 » 04 Avr 2019, 19:59
Ah ouais merci ! J'ai pas vu la disjonction de cas ça permet d'enlever r+p/q je m'en rappelerai !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités

