Dénombrement

[jean78]

Bonjour

J'ai un soucis pour compter. Voici le problème : on a des tiroirs de x couleurs différentes. De plus, il peut y avoir plusieurs tiroirs d'une même couleur (on peut appeler le nombre de tiroirs d'une même couleur c n_c).
Nous avons un nombre de balles N, chaque balle étant numéroté. On répartit ces balles dans les tiroirs de façon aléatoire. On note N_c le nombre de balles dans les tiroirs de couleur c.
La question est : quel est le nombre de cas possible pour ce rangement (fonction de N_c et n_c)?

Merci par avance pour votre aide.

[Ben314]

Salut,
Je comprend pas grand chose :
1) Concernant ce qu'on doit compter (c'est à dire quels sont les dispositions qu'on va considérer comme "identiques")
2) Concernant les chose connues au départ : d'un coté tu dit que la répartition est "aléatoire" et d'un autre qu'on doit donner la réponse "en fonction de N_c" (=le nombre de boules dans les tiroir de couleur c) ce qui me semble pas mal contradictoire l'un avec l'autre.

Peut tu donner un exemple concret de ce que tu cherche à dénombrer (i.e. avec des valeurs numériques pour les trucs "connus" et la valeur numérique du résultat)

[jean78]

Merci pour ta réponse.

Prenons 1 tiroir bleu et 2 tiroirs rouges.
Nous avons 5 balles numérotées, et nous aimerions connaître le nombre de façons de mettre 2 balles dans les tiroirs rouges.

Ici, on peut mettre soit les balles 1 et 2 dans le premier tiroir rouge, soit ces balles dans le 2e tiroir, soit la balle 1 dans l'un et l'autre balle dans le 2e, soit les balles 2 et 3 .......

Ici le total ferait C(5;2) * 4 = 40 je crois, où C(n;k) est le coefficient binomial.

J'espère que c'est plus clair.

[Ben314]

Je pense avoir compris (*)

Pour raisonner sur un exemple (c'est toujours plus clair), mettons que tu ait
- Un total de 30 balles numérotées de 1 à 30
- 4 tiroir Rouge (discernables) qui doivent au final contenir 15 balles (à eux 4)
- 3 tiroir Vert (discernables) qui doivent au final contenir 10 balles (à eux 3)
- 2 tiroir Vert (discernables) qui doivent au final contenir 5 balles (à eux 2)

Alors

1) Tes 30 balles, il faut commencer par regarder le nombre de façons de les scinder en trois groupes, l'un de 15 balles, un deuxième de 10 balles et un troisième de 5 balles.
Là, c'est un "grand classique" et il y a même un nom dédié. Ça s'appelle un coefficient multinomial <- lien (qui est la généralisation naturelle du bien connu coefficient binomial)
Ici c'est le coeff. multinomial .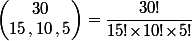

2) Ensuite, les 15 balles choisies pour aller dans les tiroirs Rouges , il faut regarder le nombre de façons de les répartir. Vu qu'il y a 4 tiroirs, ça signifie que pour chacune des balles tu as 4 possibilités et ça te fait un total de possibilités de répartitions. Idem pour les tiroirs verts et les tiroirs bleu.

Donc un total de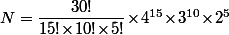

(*) Sauf que je suis pas sûr que c'est effectivement ça que tu veut dénombrer, donc je t'incite fortement à regarder pour de "tout petit cas" si ça donne bien ce auquel tu t'attend. Et si c'est pas bon, ben c'est... que j'ai pas compris correctement le problème... (les calculs, je suis à peu près certain qu'ils sont corrects)

[jean78]

Oui c'est ça je te remercie !

Bonne soirée.