Dénombrement avec répétitions "limitées"

[bobo696]

Bonjour à tous ! merci de m'accueillir parmi vous :)

Je ne suis pas étudiant en maths, mais j'ai actuellement un probleme qui pourrait etre transposé comme cela :

Soit un zoo avec 10 emplacements numérotés pouvant contenir 1 animal chacun.
Il y a 3 classes d'animaux (avec des sous classes espèces)
classe 1 félins : lion, tigre, leopard
classe 2 singes : macaque, chimpanzé
classe 3 oiseau : perroquet

La question est : combien d'arrangements possibles (l'ordre compte) existe t il, en sachant qu'au total il y aura 4 félins, 4 singes, et 2 oiseaux.

Je suis un peu perdu, car ce n'est ni arrangement sans répétitions, ni arrangements avec répétition, et en plus il y a des classes et des sous classes...

merci pour votre précieuse aide !

[Finrod]

Je ne suis pas étudiant en maths [...] Soit un zoo [...]

Tu bosses dans un Zoo ?

Il me semble que ta réponse est

[Ben314]

Salut,
Vu la façon dont je comprend l'énoncé, notre ami fait une distinction entre les répartitions :
(lion,lion, tigre, tigre,...) ET (lion, tigre, tigre, tigre,...)
par contre il ne fait pas de distinction entre
(lion,lion, tigre, tigre,...) ET (lion, tigre, lion, tigre,...)

Si c'est bien le cas, la réponse de Finrod : (c'est ce que l'on appelle un coefficient multinomial) est à multiplier par les nombres de choix des animaux dans chaque classe.

Si une classe contient sous classes et que l'on veut avoir animaux de cette classe, on doit donc compter le nombre de -uplets tels que 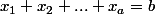(avec ) ce qui revient à placer 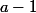"séparateurs" dans une suite de "cases".
Il y a donc choix possibles.

Conclusion, pour moi, le nombre de solutions au problème est :

[bobo696]

merci pour votre aide précieuse! Non je ne bosse pas dans un zoo, c'était histoire d'avoir une illustration visuelle du probleme, qui n'a rien a voir avec les animaux ;)

cependant, j'ai du mal expliquer dans l'énoncé :

{lion tigre lion lion} serait un arrangement différent de {lion lion tigre lion}
c'est pour cela que j'ai dis "l'ordre compte"

Est ce que cela change beaucoup vos réponses ?

[Ben314]

Ben... Forcément, ça change pas mal le résultat...

Le choix possibles pour les animaux d'une classe contenant sous classes et à remplacer par (pour chacune des cages, il y a choix possible)

Le nombre de solutions au problème est alors :

[bobo696]

merci Ben pour tes réponses rapides. J'ai compris le dernier message pour les différents choix possibles. Cependant, pour en revenir a la réponse du début, je ne comprends pas le

j'aurais interprété par : je choisi 4 individus de classe 1 pour 10 emplacements, puis 2 individus de classe 3 dans les 6 emplacements restants. Mais je ne pense pas que ce soit ca, puisqu'il y a également la derniere classe. Quelle est l'interprétation "en mots ?"

EDIT : En lisant sur wikipedia, il me semble que je devrais plutot aller dans la section : Arrangements (choix en tenant compte de l'ordre), car dans mon probleme, l'odre d'apparition compte également :

exemple {emplacement n°1 emplacement n°2} {lion tigre} est différent de {tigre lion} puisque dans le premier lion est dans l'emplacement 1 et dans le 2e lion est dans l'emplacement 2

Il me semble donc qu'il ne faudrait pas utiliser combinatoire, mais plutot arrangement, non ?

[Ben314]

Ici, la "logique du calcul" est de commencer par choisir les cages attribuées à chaque classes, PUIS quels sont les animaux que l'on choisi de mettre dans chaque cage.

Le nombre est le nombre de choix pour l'attribution des cages aux classes.
Dans cette formule, il correspond aux choix des 4 cages parmi 10 pour les
félins puis de 2 cages parmi les 6 restantes pour les oiseaux. Si tu veux, tu peut multiplier par pour les choix des 4 cages des singes parmi les 4 restanttes.

La troisième formule que je t'ai donné : permet de mieux voir la complète symétrie entre les trois nombres 4,4 et 2.

Pour le moment (choix des cages pour chaque classe) ce sont bien des combinaisons (et pas des arangements) que l'on doit faire : "mettre des singes dans les cases 1,2,3 et 4" est bien évidement identique à "mettre des singes dans les cages 4,1,2 et 3" !!!

[bobo696]

merci beaucoup pour ton aide ! Je pense avoir compris à présent :)

[Finrod]

Je demandais pour le Zoo car j'ai déjà répondu à un type qui posait une question pour son boulot. Il essayait de présenter ça comme un exo, mais bon, il s'était un peu raté et il posait des questions bizarres.

D'ailleurs ma réponse fut finalement non mathématiques.

Non mais si un des tigres fait un exéma local, c'est surement du au stress, il faut éviter de le placer près de la cage des singes, ils lui jettent des cacahouètes...

[bobo696]

Pas de probleme ! Je suis biologiste, donc je bosse presque dans un zoo ;)

Désolé mais en fait je viens de me rendre compte que ma question était incomplete :

Les enclos numérotés de 1 à 10 sont également classés par taille : 3 enclos de 2m², 5 enclos de 3m² et 2 enclos de 4m²

Donc en fait, l'ensemble N=10 est lui meme subdivisé en 3 sous ensembles de 3,5, et 2.

Exemple : 2 félins et un singe dans les enclos de 2m², 3 singes et 1 oiseau dans les enclos de 3m², et 1 félin et 1 oiseau dans les enclos de 4m²
Par contre, cette fois effectivement, on ne différencie pas les différents "ordres" de chaque classe d'animaux au sein d'un meme enclos :
{lion tigre lion} dans les enclos de 2m² sera identique a {lion lion tigre} et {oiseau macaque lion} est équivalent à {macaque lion oiseau}


Question finale : combien y a t'il de combinaisons différentes avec ces sous ensembles ?

(j'espere que ca reste compréhensible...)

[Finrod]

en sachant qu'au total il y aura 4 félins, 4 singes, et 2 oiseaux.

ceci reste-t-il valable ?

(ça fait beaucoup de cas à étudier)

[bobo696]

oui la condition 4 singes + 4 félins + 2 oiseaux doit etre respectée !

(oui je sais je suis désolé je n'ai pas bien formulé la question au début :s)

[fatal_error]

salut,

t'es pas très cohérent.

Les enclos numérotés de 1 à 10 sont également classés par taille : 3 enclos de 2m², 5 enclos de 3m² et 2 enclos de 4m²

Par contre, cette fois effectivement, on ne différencie pas les différents "ordres" de chaque classe d'animaux au sein d'un meme enclos :
{lion tigre lion} dans les enclos de 2m² sera identique a {lion lion tigre} et {oiseau macaque lion} est équivalent à {macaque lion oiseau}

Dans un enclos, on peut mettre combien de bêtes!
Au début tu dis que ya 10 enclos, et apres tu dis qu'on peut foutre trois betes par enclos.

Ce que je comprends plutot, c'est qu'on a 10 cages, et chacune d'entre elles contient 1 animal.
Et on a trois enclos de type différent. Le premier contient les trois cages de 2m^2, le second les cinq cages de 3m^2 et le troisieme les deux cages de 4m^2.

A l'intérieur de ces enclos, on ne s'intéresse pas à la disposition des animaux.


On peut proposer la formule suivante, si lion1 est considéré différent de lion2 (cqui est quand même cohérent si on considère un lionceau et un lion a trois pattes, voire un mouton diabétique).

On a 10 animaux, ca on touche pas.
Le premier en cage 1, le second en cage 2,...
On permute les animaux dans les cages :
10! possibilités

Ensuite, a lintérieur des cages, on ne se préoccupe pas de l'ordre des cages donc on a


Ou compte le nombre de mains non ordonné de 10 animaux qu'on peut faire sachant qu'on a quatre félins et quatre macaques et deux perroquets.



Au final, je compte donc
possibilités

[bobo696]

Merci fatal error pour ta réponse. Effectivement je me rends compte que je ne suis vraiment pas clair ! on ne peut mettre qu'un animal dans un enclos.

J'avais plus ou moins trouvé cette réponse (multiplié les mains non ordonnées de 10 animaux par les permutations sans répétition)

Mais ! J'ai encore une condition, lion 1 est identique à lion 2 au sein d'un meme groupe d'enclos...

Je pense que la, il s'agit donc de trouver une formule qui fait état de la probabilité d'avoir x individus d'une meme espece dans le meme groupe d'enclos ?