BNS SVP aidez moi pour resoudre ça merciii d avanceee
F: E==>E
Soit F une application de E dans E
Montrer que
(F est injective) <==> (∀ (x,y)∈ (P(E))²
F(x∩y)= F(x)∩f(y)
svp aidez moi
Demontrer que F EST UNE APLICATION INJECTIVE SVPP
6 messages
- Page 1 sur 1
Re: demontrer que F EST UNE APLICATION INJECTIVE SVPP
par double inclusion, il y a un sens facile et le second, on part d'un élément de l'ensemble F(x)∩f(y), il pourrait avoir 2 antécédents différents (ou plus), mais c'est pas possible ici
Re: demontrer que F EST UNE APLICATION INJECTIVE SVPP
bonsoir,
montrons que \subset f(x) \cap f(y))
soit)
 tel que
tel que )
 \in f(x))
 \in f(y))
donc \in f(x) \cap f(y))
donc \cap f(y))
donc \subset f(x) \cap f(y))
supposons f injective
soit \cap f(y))
=v)
=v)
donc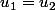

donc)
donc \cap f(y) \subset f(x \cap y))
donc \cap f(y) = f(x \cap y))
réciproque
supposons que \cap f(y) = f(x \cap y))
et montrons que f est injective:
soit=f(u_2))
) et
et )
 \cap f(\{u_2\}))
)
donc
donc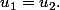
montrons que
soit
donc
donc
donc
supposons f injective
soit
donc
donc
donc
donc
réciproque
supposons que
et montrons que f est injective:
soit
donc
donc
Re: demontrer que F EST UNE APLICATION INJECTIVE SVPP
tu peux poser des questions si ça te parait indigeste 

Re: demontrer que F EST UNE APLICATION INJECTIVE SVPP
hahahaha heureusement que ya toi MALOXE pour les indigestion en math 

6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
