Démontrer que Béta est injective et surjective
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cpS
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 16:32
-
 par cpS » 28 Oct 2013, 13:01
par cpS » 28 Oct 2013, 13:01
arnaud32 a écrit:regardes du cote de
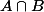
est-ce que c'est bon si je dis que la condition est: E=A=B ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2013, 13:03
par arnaud32 » 28 Oct 2013, 13:03
cpS a écrit:est-ce que c'est bon si je dis que la condition est: E=A=B ?
non
si A=B=E
comment avoir beta(X)=(E,Vide) ? (la seule solution est E=vide)
-
cpS
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 16:32
-
 par cpS » 28 Oct 2013, 13:05
par cpS » 28 Oct 2013, 13:05
arnaud32 a écrit:non
si A=B=E
comment avoir beta(X)=(E,Vide) ? (la seule solution est E=vide)
Donc comme condition je mets E= ensemble vide ?
mais après on me demande de le démontrer , comment faire?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2013, 13:09
par arnaud32 » 28 Oct 2013, 13:09
cpS a écrit:Donc comme condition je mets E= ensemble vide ?
mais après on me demande de le démontrer , comment faire?
non la condition de surjectivite est

-
cpS
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 16:32
-
 par cpS » 28 Oct 2013, 13:12
par cpS » 28 Oct 2013, 13:12
arnaud32 a écrit:non la condition de surjectivite est

Daccord. Merci
Comment le démontrer?
Pouvez-vous me donner des indications svp?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2013, 13:17
par arnaud32 » 28 Oct 2013, 13:17
pour la codition necessaire regardes
))
pour la condition suffisante, tu prends
)
et
)
et tu regardes

-
WhiteShadow
- Membre Naturel
- Messages: 63
- Enregistré le: 09 Aoû 2013, 14:06
-
 par WhiteShadow » 28 Oct 2013, 13:20
par WhiteShadow » 28 Oct 2013, 13:20
Oups, j'efface. Pardon, je me suis embrouillé.
-
cpS
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 16:32
-
 par cpS » 28 Oct 2013, 13:23
par cpS » 28 Oct 2013, 13:23
arnaud32 a écrit:pour la codition necessaire regardes
))
pour la condition suffisante, tu prends
)
et
)
et tu regardes

ça correspond à quoi Béta-1 ? La fonction réciproque?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2013, 13:28
par arnaud32 » 28 Oct 2013, 13:28
cpS a écrit:ça correspond à quoi Béta-1 ? La fonction réciproque?
oui la reciproque
tu suppose beta surjective, ce qui justifie l'existence de ce X (qui n'est pas necessaire ment unique)
-
cpS
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 16:32
-
 par cpS » 28 Oct 2013, 14:15
par cpS » 28 Oct 2013, 14:15
arnaud32 a écrit:non la condition de surjectivite est

Mais comment prouvez-vous que la condition est AnB= ensemble vide ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2013, 14:30
par arnaud32 » 28 Oct 2013, 14:30
cpS a écrit:Mais comment prouvez-vous que la condition est AnB= ensemble vide ?
tu suppose bet a surjective et tu peux donc trouver x tel que:
))
tu as donc

et

de

tu deduis que
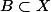
donc

donc finalment:
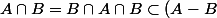\cap B =\empty)
-
cpS
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 16:32
-
 par cpS » 28 Oct 2013, 14:35
par cpS » 28 Oct 2013, 14:35
arnaud32 a écrit:tu suppose bet a surjective et tu peux donc trouver x tel que:
))
tu as donc

et

de

tu deduis que
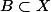
donc

donc finalment:
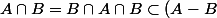\cap B =\empty)
D'accord mais lorsque que l'on me demande de démontrer que cette condition est suffisante pour dire que Béta est surjective, que dois-je écrire? ce que vous venez de marquer?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Oct 2013, 14:41
par arnaud32 » 28 Oct 2013, 14:41
cpS a écrit:D'accord mais lorsque que l'on me demande de démontrer que cette condition est suffisante pour dire que Béta est surjective, que dois-je écrire? ce que vous venez de marquer?
ca ca prouve que la condition est necessaire
elle est aussi suffisante: supposons

soit
)
et
)
tu poses

=( (a\cup b)\cap A, (a\cup b)\cap B)=)=( (a \cap A)\cup (b \cap A) , (a \cap B)\cup (b \cap B) )=( a\cup \empty, b\cup \empty)=(a,b))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 139 invités
et
tu deduis que
donc