Bonjour à tous,
je lisais une preuve de l'existence de la factorisation de Cholesky pour une matrice hermitienne définie positive, à savoir pour une matrice hermitienne définie positive

il existe une unique matrice triangulaire supérieure à coefficients diagonaux positifs

telle que

.
Dans cette preuve on utilise le fait que

admet une décomposition
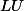
(car tous ses mineurs sont positifs), où

est triangulaire inférieure et

est triangulaire supérieure.
La décomposition n'est pas unique si on impose pas que

soit unitaire je crois.
Après on fait intervenir une matrice

diagonale telle que
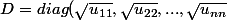)
de manière à pouvoir écrire
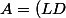(D^{-1}U))
. En fait, c'est là que j'ai un souci car pourquoi tous les coefficients diagonaux de

seraient-ils positifs pour pouvoir prendre leurs racines ?
Est-ce bien parce que si jamais un des
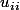
est tel que
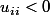
alors on peut quand même trouver une décomposition
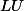
pour

avec

à coeffs diagonaux positifs.
Par exemple si
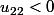
on a
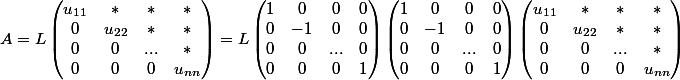
Et en notant

et
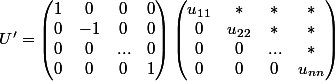
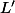
reste bien triangulaire inf,
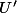
triangulaire sup et on a bien
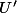
à coeffs diagonaux positifs avec
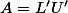
J'ai bon ?
