Matrice définie positive et symétrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Mar 2009, 15:36
par Nightmare » 23 Mar 2009, 15:36
Bonjour :happy3:
Je vous propose un exercice d'oral de l'X très jolie dans sa solution. (source : Leichtam)
Montrez que la matrice
_{1\le i,j\le n})
est définie positive et symétrique
Amusez-vous bien!
:happy3:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 23 Mar 2009, 17:27
par Joker62 » 23 Mar 2009, 17:27
La symétrie je sais faire :)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Mar 2009, 17:31
par Nightmare » 23 Mar 2009, 17:31
Je suis sûr qu'il y en a qui plancheraient quand même un quart d'heure sur la symétrie :lol3:
Au contraire, il y en a qui torcheraient le caractère définie positif en 2 minutes et ça c'est rageant :lol2:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 23 Mar 2009, 17:38
par Joker62 » 23 Mar 2009, 17:38
Pour la définie positivité, j'ai ressorti un vieux cours d'analyse matricielle lol
[MODE n'imps]La matrice est à diagonale strictement dominante
Les coeffs de la diagonales sont tous positifs
Donc la partie réelle des valeurs propres est positive
Comme elle est symétrique, les valeurs propres sont réelles et sont toutes positives strictement.[/Mode n'imps]
Désolé la matrice n'est pas à diagonale strictement dominante

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Mar 2009, 17:49
par Nightmare » 23 Mar 2009, 17:49
Ca aurait pu marcher :lol3:
Au lieu de sortir un vieux cours d'analyse matricielle, sort plutôt un cours d'analyse tout court :lol3:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 23 Mar 2009, 18:04
par yos » 23 Mar 2009, 18:04
vp évidente :
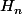
.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Mar 2009, 19:12
par Nightmare » 23 Mar 2009, 19:12
Et sans calcul de vp?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 23 Mar 2009, 20:01
par ThSQ » 23 Mar 2009, 20:01
C'est pas la seule vp.
Sans détail vu que c'est dans le Leichtman (d'après Nightmare) et que c'est largement inspiré du même résultat sur la matrice de Hilbert (
http://fr.wikipedia.org/wiki/Matrice_d%C3%A9finie_positive ) :
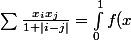 dx)
avé
 = \sum x_i x_j x^{|i-j|})
Suffit de montrer que f(x) > 0 pour 0 < x < 1 ce qui se fait par récurage par ex.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Mar 2009, 21:34
par Nightmare » 23 Mar 2009, 21:34
Par récurage?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 23 Mar 2009, 22:49
par yos » 23 Mar 2009, 22:49
ThSQ a écrit:C'est pas la seule vp.
Ah oui, ça prétendais pas plier l'exo.
Pour n=2 et 3, les vp sont toutes rationnelles. Au delà faudrait regarder.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Mar 2009, 18:37
par ThSQ » 24 Mar 2009, 18:37
Nightmare a écrit:Par récurage?
Tu n'as jamais fait de raisonnement par récurage ? On en sort lessivé bien souvent

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
est définie positive et symétrique
est définie positive et symétrique