J'ai bien évidemment fait quelques recherches mais je ne trouve rien.
Convexité fonction 2 variables
6 messages
- Page 1 sur 1
Convexité fonction 2 variables
Bonsoir, je dois prouver qu'une fonction est convexe . Vu qu'elle est un peu complexe je pense que la subdiviser en 3 fonctions est le meilleur moyen. Ensuite passer par la matrice hésienne de chaque fonctions . Le seul problème est que je ne comprend pas comment faire la dérivée (sachant que alpha,beta,y sont des vecteurs et x est une matrice). Et phi est la fonction sigmoid
J'ai bien évidemment fait quelques recherches mais je ne trouve rien.
 =<br />- \sum_{i=1}^{n} \left [ y_{i1} \log(\phi(\alpha_1 + \beta^T x_i)) <br />+ \sum_{j=2}^{k-1} \Big( y_{ij} \log( <br />\phi(\alpha_j + \beta^T x_i) - \phi(\alpha_{j-1} + \beta^T x_i)) \Big)<br />+ y_{ik} \log(1 - \phi(\alpha_{k-1} + \beta^T x_i)) \right ] $)
J'ai bien évidemment fait quelques recherches mais je ne trouve rien.
Re: Convexité fonction 2 variables
Salut,
Ca me semble quand même être le B-A-BA de la logique que de comprendre que sans savoir ce que représentent (concrètement) les différentes variables apparaissant dans la fonction, donc savoir à quelle domaine elles appartiennent (voire ce que représente la fonction elle même), ben on risque pas de dire quoi que ce soit.
Déjà, rien que le logarithme de la somme du milieu impose des conditions sur les variables/constantes pour que la formule ait du sens (1) et c'est bien évidement la même chose concernant la convexité : par exemple, le truc qui saute aux yeux, c'est que le bidule est linéaire par rapport à la matrice des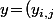_{i,j}) (2) et qu'évidement, ça signifie que, si pour une certaine matrice
(2) et qu'évidement, ça signifie que, si pour une certaine matrice  , la fonction est convexe, alors pour la matrice opposée
, la fonction est convexe, alors pour la matrice opposée 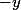 , la fonction sera concave.
, la fonction sera concave.
(1) Par exemple, ça a l'air d'être vrai, mais c'est pas franchement clair que le domaine de définition de ta fonction f, est bien convexe. Et évidement, de parler de "fonction convexe" sur un domaine non convexe, ben ça veut plus rien dire !!!
(2) Et je suppose que c'est un lapsus d'avoir écrit que "y est un vecteur"
Ca me semble quand même être le B-A-BA de la logique que de comprendre que sans savoir ce que représentent (concrètement) les différentes variables apparaissant dans la fonction, donc savoir à quelle domaine elles appartiennent (voire ce que représente la fonction elle même), ben on risque pas de dire quoi que ce soit.
Déjà, rien que le logarithme de la somme du milieu impose des conditions sur les variables/constantes pour que la formule ait du sens (1) et c'est bien évidement la même chose concernant la convexité : par exemple, le truc qui saute aux yeux, c'est que le bidule est linéaire par rapport à la matrice des
(1) Par exemple, ça a l'air d'être vrai, mais c'est pas franchement clair que le domaine de définition de ta fonction f, est bien convexe. Et évidement, de parler de "fonction convexe" sur un domaine non convexe, ben ça veut plus rien dire !!!
(2) Et je suppose que c'est un lapsus d'avoir écrit que "y est un vecteur"
Modifié en dernier par Ben314 le 22 Déc 2018, 14:21, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Convexité fonction 2 variables
@mathelot il y a seulement un crochet manquant à la fin de l'équation
@ben314 excuse moi tu as raison donc par rapport à Y c'est une variable aléatoire discrète du coup pour Y1=1 on a y1j = [1.0.0] (c'est sensé être la classe de la ligne 1 vu que c'est un problème de classification) et on a les alpha croissant càd alpha_i<alpha_i+1 sinon il n y a pas de conditions sur les x
@ben314 excuse moi tu as raison donc par rapport à Y c'est une variable aléatoire discrète du coup pour Y1=1 on a y1j = [1.0.0] (c'est sensé être la classe de la ligne 1 vu que c'est un problème de classification) et on a les alpha croissant càd alpha_i<alpha_i+1 sinon il n y a pas de conditions sur les x
Re: Convexité fonction 2 variables
Dans ce cas là, et comme je l'ai déjà écrit dans le précédent post, c'est réglé : si tu ne sait rien sur les signes des 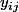 , tu n'a pas la moindre chance d'arriver à montrer que ta fonction est convexe vu que de remplacer les
, tu n'a pas la moindre chance d'arriver à montrer que ta fonction est convexe vu que de remplacer les 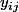 par leur opposé change l'éventuelle convexité en concavité.
par leur opposé change l'éventuelle convexité en concavité.
P.S. Quoi que, vu le truc que tu raconte avec ton Y1=1 "donc" y1j = [1.0.0] (dont je comprend pas trop le sens), tu est sûr que tes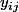 c'est bien des variables aléatoires et pas plutôt des probabilités de valeur de certaines variables aléatoires ?
c'est bien des variables aléatoires et pas plutôt des probabilités de valeur de certaines variables aléatoires ?
Rappel (du vocabulaire) : Quand on jette un dés, le résultat que donne le dés (donc un entier entre 1 et 6), c'est une variable aléatoire (discrète). Et les nombres 1/6 ; 1/6 ; ... 1/6 (de somme =1), ce sont les différentes probabilités que cette variable aléatoire prenne les valeurs 1,2,3,4,5,6
P.S. Quoi que, vu le truc que tu raconte avec ton Y1=1 "donc" y1j = [1.0.0] (dont je comprend pas trop le sens), tu est sûr que tes
Rappel (du vocabulaire) : Quand on jette un dés, le résultat que donne le dés (donc un entier entre 1 et 6), c'est une variable aléatoire (discrète). Et les nombres 1/6 ; 1/6 ; ... 1/6 (de somme =1), ce sont les différentes probabilités que cette variable aléatoire prenne les valeurs 1,2,3,4,5,6
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Convexité fonction 2 variables
dans mon cas j'ai 3 cas. Y=1 Y=2 Y=3
pour Y=1 y=[1,0,0] , Y=2 y=[0,1,0] , Y=3 y=[0,0,1]
yij est toujours >=0 elle prend 0 ou 1 et la somme des yij sur j est1
pour Y=1 y=[1,0,0] , Y=2 y=[0,1,0] , Y=3 y=[0,0,1]
yij est toujours >=0 elle prend 0 ou 1 et la somme des yij sur j est1
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
