Bonjour, si on se fixe x>0 et qu'on pose f_0(x) = x et pour tout n, f_n+1(x)= 1/2 (f_n(x)+x/f_n(x)) , alors on a pas de mal à montrer que f_n(x) tend vers racine de x quand n tend vers + infini (suite récurrente classique).
Maintenant si on étudie la convergence uniforme de la suite de fonction (f_n) vers la fonction racine, sur tout segment pas de problème la réponse est oui. Sur un voisinage de +infini, en revanche, j'ai des doutes....à la fois la convergence de la méthode de Héron est rapide, et à la fois quand x est grand , on ne majore plus aussi facilement le |f_n(x)-sqrt(x)|. Je pencherais plutôt pour la non convergence uniforme mais j'ai du mal à la montrer. La suite n'étant pas explicite ce n'est pas facile de raisonner avec des contre-exemples, il faudrait plutôt minorer f_n(x) - sqrt(x) mais je n'arrive à rien de concluant.
Quelqu'un aurait il une idée?
Convergence uniforme de la "méthode de Héron"
3 messages
- Page 1 sur 1
Re: convergence uniforme de la "méthode de Héron"
Salut,
Lorsque tend vers
tend vers  ,
, ) est équivalent à
est équivalent à  (preuve par récurrence) donc
(preuve par récurrence) donc \!-\!\sqrt{x}) tend vers
tend vers  et cela prouve que la suite
et cela prouve que la suite _{n\geqslant 0}) ne converge uniformément vers
ne converge uniformément vers  sur aucun intervalle
sur aucun intervalle 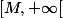 .
.
Lorsque
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
