Méthode de Héron

[Tyson13]

Bonjour,

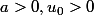
Soit et

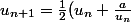Dans les questions précédantes j'ai déjà démontrer que :
1).

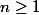
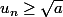
2)pour , et est décroissante.

3) converge vers .

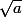
4)


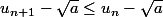
Je bloque sur la question 5.

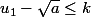
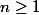
5) Si et pour montrer que :




J'essaie de démontrer par récurrence :

Pour n = 1 , OK on tombe sur l'hypothèse avec k.

d'après 4 j'ai :

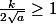
Le problème étant qu'il faudrait montrer que pour conclure.

[Maxmau]

Bonjour,

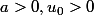
Soit et

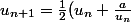Dans les questions précédantes j'ai déjà démontrer que :
1).

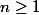
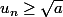
2)pour , et est décroissante.

3) converge vers .

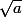
4)


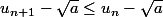
Je bloque sur la question 5.

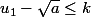
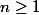
5) Si et pour montrer que :




J'essaie de démontrer par récurrence :

Pour n = 1 , OK on tombe sur l'hypothèse avec k.

d'après 4 j'ai :

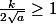
Le problème étant qu'il faudrait montrer que pour conclure.

Bj
Je pose racine(a) = L
U(n+1) = (1/2)(Un + L²/Un)
L = (1/2)(L + L²/L)
En soustrayant membre à membre U(n+1) - L = (1/2Un)(Un - L)²
d'où: U(n+1) - L < (1/2L)(Un - L)²
avec cette inégalité je pense que tu peux montrer 5: par récurrence

[Tyson13]

avec l'inégalité je me retrouve avec :



Mais je vois pas quoi faire ensuite ?

[Maxmau]

avec l'inégalité je me retrouve avec :



Mais je vois pas quoi faire ensuite ?

on a vu que: U(n+1) - L < (1/2L)(Un - L)²
supposons (hyp de récurrence) que: Un - L < 2L (k/2L)^(2^(n-1)
alors: U(n+1) - L < (1/2L)[2L(k/2L)^(2^(n-1)]²
soit: U(n+1) - L < (1/2L)[4L² (k/2L)^(2^n)]
d'où U(n+1) - L < 2L (k/2L)^(2^n)
Comme l'inégalité est vraie pour n=1, elle est démontrée par récurrence