Convergence de suite trigonométrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 15 Oct 2022, 09:09
par ThomasScc » 15 Oct 2022, 09:09
Bonjour,
J'ai un devoir maison à rendre et j'avoue être pas mal perdu!
En particulier cet exercice du dm:

Je suis bloqué dès la première question. On nous demande la limite de cos^2(na)) sauf que la fonction cos(x) n'a pas de limite en +infini, donc par déduction je suis tenté de dire que cos^2(x) n'en a pas non plus (et donc cos^2(na) idem)
Merci d'avance à ceux qui auraient des pistes
Modifié en dernier par
ThomasScc le 15 Oct 2022, 22:18, modifié 1 fois.
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 15 Oct 2022, 12:27
par phyelec » 15 Oct 2022, 12:27
Bonjour,
pour la question 1) utilisez la formule trigo
+sin^2(x)=1)
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 15 Oct 2022, 15:05
par ThomasScc » 15 Oct 2022, 15:05
Oui c'est ce que j'avais fait et je pense que c'est le bon raisonnement finalement, j'avais pas fait gaffe que l'énoncé posait directement l comme la limite de sin(na)
cos^2+sin^2=1 donc cos^2=1-sin^2 Donc la limite de cos^2(nx) = 1-l^2 en prenant l^2= la limite de sin^2(na)
Pour la deuxième question ils demandent d'utiliser cos(2na). Donc j'imagine qu'il faut utiliser la formule cos(2x)=cos^2(x)-sin^2(x) (ou une des 3 autres?)
Est-ce que la formule est toujours exacte si je remplace simplement les x par des na ?
Dans ce cas on aurait cos(2na)=cos^2(na)-sin^2(na) mais je sais pas trop quoi en faire
Modifié en dernier par
ThomasScc le 15 Oct 2022, 22:17, modifié 1 fois.
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 15 Oct 2022, 18:27
par phyelec » 15 Oct 2022, 18:27
Bonjour,
oui pour la première question.
pour la deuxième question :
vous avez écris cos(2na)=cos^2(na)-sin^2(na) OK
vous connaissez les limites de sin^2(na) et cos^2(na) (première question)
donc vous pouvez trouvez la limite cos(2na)
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 15 Oct 2022, 19:05
par ThomasScc » 15 Oct 2022, 19:05
Bonsoir
cos^2(na)= 1-sin^2(na)
sin^2(na)=1-cos^2(na)
donc limite de cos(2na) = (1-sin^2(na))-(1-cos^2(na))= -sin^2(na)+cos^2(na)=?
Or cos(2na)=1-2sin^2(na) équivaut à sin^2(na)=(1-cos(2na))/2 donc pour avoir sin^2(na)=0 (ce qu'on cherche car on cherche à montrer que l=0=sin(na)) on doit avoir cos(2na)=1
Mais -sin^2(na)+cos^2(na) ne peut pas valoir 1 si sin^2(na)+cos^2(na)=1
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 15 Oct 2022, 21:39
par phyelec » 15 Oct 2022, 21:39
avec la formule
=\cos^2(na)-\sin^2(na))
vous pouvez écrire :
)=\lim (cos^2(na))- \lim(sin^2(na))= \lim (\cos^2(na))-\lim(\sin(na))*\lim(\sin(na)))
soit :
)= 1 - l^2 -l*l=1-2l^2)
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 15 Oct 2022, 22:04
par ThomasScc » 15 Oct 2022, 22:04
Ahh en effet ! Au début je voulais bien utiliser le l pour la limite de cos(2na) mais j'étais bloqué sur la limite de sin^2(na) alors que c'est juste l*l
Ok donc on a lim(cos(2na))=1-2l^2. Mais j'ai beau chercher je ne vois pas comment le relier au reste du problème et surtout à sin(na)

Même en utilisant une formule qui implique les 2 je me retrouve juste avec sin(na)=l^2 ce que je sais déjà..
A la limite si je pouvais exprimer en fonction de l une fonction dont je connais déjà la limite en +infini ce serait plus simple, sauf que cos(x) et sin(x) n'ont pas de limite en +infini donc c'est pas pratique
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 15 Oct 2022, 22:51
par phyelec » 15 Oct 2022, 22:51
faites le changement de variable N=2n et dites ce que vaut la limite de sin(Na) et cos(Na) quand N tend vers l'infini
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 15 Oct 2022, 23:18
par ThomasScc » 15 Oct 2022, 23:18
lim(sin(Na))=l
lim(cos(Na))=racine(1-l^2)
J'y comprends rien aux fonctions trigonométrique je vais finir par abandonner
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 16 Oct 2022, 11:43
par phyelec » 16 Oct 2022, 11:43
oui c'est cela. Regardez pour quelle valeur de l vous avez l'égalité
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 16 Oct 2022, 12:34
par ThomasScc » 16 Oct 2022, 12:34
(cos(Na))=racine(1-l^2)
1-l^2 = cos^2(Na)
l^2 = 1-cos^2(Na)
l= rac(1-cos^2(Na))
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 16 Oct 2022, 14:35
par phyelec » 16 Oct 2022, 14:35
n'oubliez pas, il s'agit de limite.
vous avez :
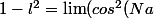)=\lim(cos^2(2na)))
et vous connaissez
)=1-2l^2)
je vous laisse terminer
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 16 Oct 2022, 14:49
par ThomasScc » 16 Oct 2022, 14:49
Je prends le carré de (1-2l^2) et je trouve 1-4l^2+4l^4.
Ce qui doit être égal à 1-l^2.
4-4l^2+4l^4=1-l^2 équivaut à 4l^4-3l^2=0
d'où l^2(4l^2-3)=0
donc l^2=0 d'où l=0
mais j'ai aussi la possibilité que l soit égale à rac(3)/2 non ?
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 16 Oct 2022, 16:13
par phyelec » 16 Oct 2022, 16:13
au fait dites-moi ce que vaut
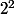
et
^2)
vous êtes sûr que

implique

?
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 16 Oct 2022, 16:26
par ThomasScc » 16 Oct 2022, 16:26
Oui évidemment c'est rac(3)/2 et -rac(3)/2, je voulais juste dire que d'autres solutions que 0 sont trouvées
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 16 Oct 2022, 16:56
par phyelec » 16 Oct 2022, 16:56
et bien oui, remplacez les solutions non nulles trouvées dans rac( 1-l^2)=1-2l^2 et concluez
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 16 Oct 2022, 17:18
par ThomasScc » 16 Oct 2022, 17:18
en remplaçant l par rac3/2 dans rac( 1-l^2)=1-2l^2 on trouve que 1/2=-1/2 donc contradiction.
Donc l différent de rac3/2 et de -rac3/2 (ce serait le même calcul)
Donc l=0
Merci !
Pour la question 3) par contre je suis largué
-
phyelec
- Habitué(e)
- Messages: 988
- Enregistré le: 06 Mar 2020, 16:47
-
 par phyelec » 16 Oct 2022, 18:19
par phyelec » 16 Oct 2022, 18:19
commencez par essayer d'utiliser sin((n+1)a) et passez à la limite
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 16 Oct 2022, 19:22
par ThomasScc » 16 Oct 2022, 19:22
sin((n+1)a)=sin(na+a)
lim(sin(na))=0
lim(sin(na+a))=0 ? na tend vers l'infini donc on peut négliger +a ?
Modifié en dernier par
ThomasScc le 16 Oct 2022, 19:29, modifié 1 fois.
-
ThomasScc
- Membre Naturel
- Messages: 15
- Enregistré le: 15 Oct 2022, 09:00
-
 par ThomasScc » 16 Oct 2022, 19:24
par ThomasScc » 16 Oct 2022, 19:24
J'ai même envie de dire lim(sin(na+a))= lim(sin(na))+lim(sin(a)) et donc 0=0+x donc sin(a)=0 mais là je pense que tous les profs de maths me tomberaient dessus pour avoir séparé en 2 le sin
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités


 Même en utilisant une formule qui implique les 2 je me retrouve juste avec sin(na)=l^2 ce que je sais déjà..
Même en utilisant une formule qui implique les 2 je me retrouve juste avec sin(na)=l^2 ce que je sais déjà..