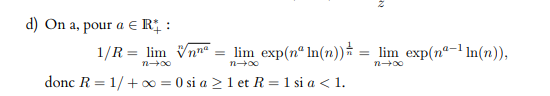[L2] Convergence de séries

[ThPra]

Bonjour!

J'ai commencé à réviser mes exams, et en regardant un peu les anciens sujets (et leur correction), j'ai trouvé des résultats qui me paraissaient pas du tout évident. Notamment sur ce qui concerne les rayons de convergence de séries, mais aussi leur somme.
Je vais mettre quelques screens en disant où je bloque:



Par exemple dans cet exercice, pour le a) je comprends le calcul de la limite, par contre je ne comprends absolument pas le -ln(2) pour la somme. En fait je ne comprends pas comment un ln(x) peut intervenir là-dedans. (J'imagine que ça vient d'un résultat type que je suis censé connaître, mais j'ai regardé dans le cours et aucune trace de logarithme)

Idem pour le b) je ne comprends pas d'où sort ce e (je comprends par contre la puissance n, on a juste multiplié 1/n par n^2.

J'ai d'autres screens mais je préfère éviter de flood, je les ajouterai après.

Merci d'avance !

[phyelec]

Bonjour ,

pour le a) est la série Harmonique dont la somme vaut ln(2). C'est un résultat connu.

[phyelec]

oups ! j'ai cliqué sur envoyer au lieu de aperçu, il faut lire pour la série:

[phyelec]

pour le b)

critère :




quand n tend vers +oo 1/n temps vers 0 donc on peut prendre le DL au premier ordre de ln(1+x) quand x tend vers 0, donc :
tend vers quand n tends vers +oo

donc :

[ThPra]

Merci beaucoup !

J'ai aussi du mal avec ce résultat:



Dans la ligne en rouge j'ai du mal à comprendre comment on est passé de 1/(n+1) à 1/n.
Je remarque qu'on a factorisé la somme par 1/z, et je ne comprends pas pourquoi on passe à n=2, et ce +1 qui disparaît m'intrigue pas mal.

Et j'ai encore une fois un problème avec le ln. Est-ce à savoir que la série de Zn/n vaut -ln(1-z) ? ou ai-je juste raté un détail de calcul ?

Merci encore pour votre aide!

[phyelec]

voici le calcul détaillé :

[phyelec]

pour le ln, il faut que dans cet exercice bien garder en tête que |z| 1, et cela a son importance car ln(1+x) et ln(1-x) ont des développements limités (usuels à connaître par cœur ainsi que les autres] pour x ]-1,1[ que je vous invite à regarder et je pense que cela vous éclairera sur la résultat de l'exercice. Si vous avez encore des soucis revenez vers moi avec votre question.

[ThPra]

Merci! Vous ne savez pas à quel point vous avez débloqué beaucoup de problèmes en évoquant les développements limités.

Ma dernière interrogation est sur cette simplification :



Je comprends quand on passe à l'exponentielle, mais je ne comprends pas comment on passe de a à a-1 en supprimant la puissance 1/n

[tournesol]

[ThPra]

Merci ! En effet je ne savais pas que ln(a^n) = n ln(a)

Bonne soirée et merci à vous deux pour vos réponses!