Convergence presque sur

par **bsangoku** » 22 Déc 2010, 19:38

Bonjour,

Je suis en L3 maths et a un problème à un question:

[HTML]Soit U une var de loi uniforme sur l'intervalle [0,1]
Pour tout nN*,
posons:

Un=(n+1)^2 Indicatrice de U sur [0,1/n] - n(n+2) Indicatrice de U sur [1/n,2/n]

Montrer que * Un----->0 ps
** E(Un)------->0
*** E(|Un|)------>0[/HTML]

J'ai réussi à faire ** et ***, cependant j'ai un problème pour montrer * (je n'arrive pas à démarrer).
Pouvez vous m'aider svp?

Merci d'avance.

Ps: C'est mon premier poste: désolé si mon Un est mal écrit.

par **girdav** » 22 Déc 2010, 19:57

Bonjour,
soit

tel que

. Alors il existe

tel que

pour

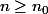
et donc

. Que peut-on dire de la probabilité de l'ensemble des

tels que

?

par **bsangoku** » 22 Déc 2010, 20:23

Avant de répondre à votre question, j'ai une autre question:
soit w tel que U(w)>0: mais pourquoi on commence par ça? Parce que je me dis que ce serai mieu de commencer par u(w)!=0

par **girdav** » 22 Déc 2010, 20:29

Parce que si

alors

et ça ne converge pas.

par **bsangoku** » 22 Déc 2010, 20:48

ok merci (c'est rare de trouver des exos sur la convergence presque sur) et pour la probabilité c'est égale à 1...

Merci...

par **girdav** » 22 Déc 2010, 21:01

Il n'y en a pas assez sur ta feuille de TD? Sinon, on doit pouvoir en trouver dans des livres.

par **bsangoku** » 22 Déc 2010, 21:43

Non il yen avait qu'un seul (dans le cas discret)...

par **girdav** » 22 Déc 2010, 21:54

Alors je te propose de regarder [url=math.univ-angers.fr/~chaumont/epdfiles/TDM14.pdf]par ici[/url].

par **bsangoku** » 23 Déc 2010, 08:25

Merci, je vais essayé de le voir dans la journée.

Convergence presque sur

Convergence presque sur

Qui est en ligne