Convergence d'intégrale

[Joker62]

[FONT=Comic Sans MS]Bonsoir tout le monde !
Donc j'suis en pleine révision analystique ( J'sais pô si ça se dit désolé :s )

Et donc j'voudrais une ptite critique sur un raisonnement que je fais pour connaître la nature d'une intégrale généralisée.

On s' intéressera à l'integrale suivante :

I =

On commence donc par étudier cette intégrale en 0 :

Soit a > 0 :
On effectue un DL en 0 de la fonction


D'où

On utilise alors le critère :


D'où l'intégrale converge


Bon après en , c'est assez basique par une majoration de par 2.

Et au final on trouve I converge

J'vous remercie de votre aide et de vos explication si j'ai fais une stupidité quelque part
Bonne nuit à tous !
[/FONT]

[Joker62]

J'ai oublié de préciser que

[BQss]

[quote="Joker62"][FONT=Comic Sans MS]Bonsoir tout le monde !
Donc j'suis en pleine révision analystique ( J'sais pô si ça se dit désolé :s )

Et donc j'voudrais une ptite critique sur un raisonnement que je fais pour connaître la nature d'une intégrale généralisée.

On s' intéressera à l'integrale suivante :

I =

On commence donc par étudier cette intégrale en 0 :

Soit a > 0 :
On effectue un DL en 0 de la fonction


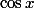
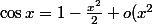D'où

On utilise alors le critère :
[TEX]\large t^{\alpha-2} \ . \ \frac {1+\epsilon(t)}{t^{\alpha-2}} \ = \ 1 + \epsilon(t) \longrightarrow_{t \rightarrow 0} 1 \ (0.
Or pour tout M appartenant à ]0;2[ M/t^(a) converge pour a>1 et diverge pour a alpha appartient à ]1;3[

Sauf erreur car c'est assez lointain, il me semble qu'il faut le preciser, d'autre sur le site te confirmerons ou pas de toute facon. Sinon c'est juste c'est la bonne methode.

*Edit
D'ailleurs, il faut faire attention en fait car 2/x est aussi une fonction comprise entre 0 strictement et 2 sur ]2;+inf[ et pourtant integrale 1/x/x^a converge pour x>0 qui est inferieur à 1.
Ma precision marche si l'on precise que la fonction 1-cost est continue et periodique.

[fahr451]

globalement c'est bien ;
une première chose :bien dire que la fonction est continue surR+* donc localement intégrable(ce qui revient à prouver que les SEULS problèmes sont en 0 et +infini )
une deuxième chose tu dois préciser le caractère POSITIF (ou de signe fixe)des fonctions (au moins localement) pour utiliser les équivalents ou petits 0 afin de conclure sur la nature des intégrales.

[BQss]

globalement c'est bien ;
une première chose :bien dire que la fonction est continue surR+* donc localement intégrable(ce qui revient à prouver que les SEULS problèmes sont en 0 et +infini )
une deuxième chose tu dois préciser le caractère POSITIF (ou de signe fixe)des fonctions (au moins localement) pour utiliser les équivalents ou petits 0 afin de conclure sur la nature des intégrales.

Quand au fait de dire qu'elle ne converge pas pour un alpha1 c'est bon). Tu as une idée plus evidente que ce que j'ai ecrit pour t'en assurer?

Par exemple si on ramplace 1-sin(t) par 2/x cela converge jusqu'a 0 exclu...
Majorer 2/x par 2 (qui est une fonction positive) ce n'est pas suffisant pour justifier l'equivalence pour alpha superieur à 1 la preuve c'est bon jusqu'a 0... Je n'ai pas trouvé d'autre methode(je pensais aussi a construire deux integrales dont un tendant vers 0 centré sur f^-1(0) mais il faudraitt bien choisir la suite E(n) pour que ]f^-1(0)-E(n);f^-1(0)+E(n)[ tende vers l'ensemble vide suffisament vite pour pouvoir dire que la limite de l'integrale privé de cet ensemble ou la fonction est minoré converge pour les meme valeurs quel'intergale que l'on etudie.


Si non oui, les fonctions sous l'integrales sont bien positives(il faut pas oublié de le preciser), il utilise implicitement cette donnée pour le probleme en +infini vu qu'il majore la fonction par 2 et la minore par 0...

[fahr451]

le fait que ce soit de la forme M(t)/t^alpha avec M(t) strictement positif inférieur à 2 ;ne prouve pas l"équivalence suivante : l'intégrale en + inf converge ssi alpha>1 le sens gauche droite n'est pas vrai.
par exemple M(t) = 1/ln^2(t) et alpha = 1, l'intégrale (de bertrand) converge au voisinage de +infini.

Moi je dirais en me limitant à 1>=alpha >0
l'intégrale de cost/t^alpha converge (en +infini) faire une intégration par partie pour se ramener à une intégrale absolument convergente
(en 1/t^(alpha+1) or l'intégrale de 1/t^alpha diverge en + inf donc l'intégrale de la somme diverge.

[BQss]

le fait que ce soit de la forme M(t)/t^alpha avec M(t) strictement positif inférieur à 2 ;ne prouve pas l"équivalence suivante : l'intégrale en + inf converge ssi alpha>1 le sens gauche droite n'est pas vrai.
par exemple M(t) = 1/ln^2(t) et alpha = 1, l'intégrale (de bertrand) converge au voisinage de +infini.

C'est ce que j'ai dit tu peux prendre plus simple que ln^2(t), j'ai pris comme exemple M(t)=1/t moi et ca converge jusqu'a 0...

Par contre le resultat est juste si l'on rajoute que M(t) est continue et periodique.

[BQss]

Moi je dirais en me limitant à 1>=alpha >0
l'intégrale de cost/t^alpha converge (en +infini) faire une intégration par partie pour se ramener à une intégrale absolument convergente
(en 1/t^(alpha+1) or l'intégrale de 1/t^alpha diverge en + inf donc l'intégrale de la somme diverge.

Ouai ok.

.............

[fahr451]

vi vi j'avais pas vu le edit

[Joker62]

Ah oui j'oublie toujours de dire que c'est localement intégrable, alors que c'est là base...

Et pour en +oo c'est vrai qu'on peut dissocer les cas ou le numérateur s'annule j'y avais pas pensé.

J'vous remercie vraiment pour tout (k)
ça fait plaisir d'avoir des réponses sûres, parce que mon prof de TD :s y'est un peu à la masse lol

[BQss]

Ah oui j'oublie toujours de dire que c'est localement intégrable, alors que c'est là base...

Et pour en +oo c'est vrai qu'on peut dissocer les cas ou le numérateur s'annule j'y avais pas pensé.

J'vous remercie vraiment pour tout (k)
ça fait plaisir d'avoir des réponses sûres, parce que mon prof de TD :s y'est un peu à la masse lol

Precise bien aussi qu'elle diverge pour alpha<=1 donc pour t'assurer de l'equivalence sur ]1;3[ ...

[Joker62]

Oui mais étant donné que est un réel strictement positif
Il me suffit juste de dire que ça converge et que ça diverge sinon... no ?

[BQss]

Oui mais étant donné que est un réel strictement positif
Il me suffit juste de dire que ça converge et que ça diverge sinon... no ?

Tu sais que ca diverge pour alpha>3
Ensuite tu montres que ca converge pour alpha >1(le probleme en +infini), mais ta demo ne dis rien pour alpha0(fahr t'as indiqué qu'on retrouvait ca avec une integration par partie) et que donc l'integrale généralisé de (1-cos(x))/x^a est egal a la somme de l'integrale de cos(x)/x^a + integrale de 1/x^a (tu as le droit de dire que l'integrale généralisé de la somme est egal a la somme des integrales car l'une des deux converge, ce sont des limites que tu traites donc tu appliques les meme formules que pour la somme des limites).
Or integrale 1/x^a diverge pour a3, a<1 et que entre les deux il n'y avait aucun probleme en 0 et + infini.
Donc cela converge sur ]1;3[

[Joker62]

Donc l'intégration par partie ça donne bien ça ?

Soit u = u' =
v' = cos(t) v = sin(t)

(intégrale de 1 à +oo) de cos t / t^a =

Bon et en effet cette deuxième intégrale converge pour a + 1 > 1 donc pour a > 0
Mais je vois pas en quoi tout ça converge vu que sin t n'a pas de limite en +oo

D'où si je vous écoute on peut décomposer l'intégrale du début en somme de deux intégrales, ( là j'ai pas compris pourquoi, je pensais que la convergence des deux intégrales étaient nécéssaires... )

Et donc l'intégrale de 1/t^a et celle de cos t / t^a qui converge si a > 1 ( Critère de Riemann pour la première )
Les deux convergent pour a > 1 et divergent pour a <= 1.

Ce qui prouve que ça converge si et seulement si a ]1;3[

[fahr451]

je ne comprends pas sur quoi porte ta question; repose là s 'il te plait

[Joker62]

Bé on est toujours sur la question de la convergence pour un a compris entre 0 et 1 inclu.

[fahr451]

j'ai répondu

on pose f(t) = 1/t^a - cost /t^a
l'intégrale de cost/t^a converge en + infini (IPP) et si l'intégrale de f convergeait alors celle de 1/t^a aussi ce qui est faux.

[BQss]

Bé on est toujours sur la question de la convergence pour un a compris entre 0 et 1 inclu.

C'est le meme systeme que pour des limites*:

si lim f ou lim g est fini alors:
lim(f+g):limf+limg
donc comme l'integrale avec le cos converge ton integrale a le meme comportement que l'integrale de 1/t^a

*on pose A=cos(t)/t^a et B= 1/t^a:
On a lim x-->+inf [integrale de 1 à t de A] = K
donc
lim x-->+inf [integrale de 1 a t de (A+B) ]
=lim x-->+inf [ integrale (A) + integrale (B)]=
=lim x-->+inf [integrale (A)] + lim x-->+inf [ integrale (B) ] car integrale de A converge
= K + lim x-->+inf [ integrale (B) ]

donc l'integrale de la somme a le comportement de l'integrale de B

[Joker62]

Ah ouai ! :)
J'voyais pas ça comme ça
Merci à tous pour votre aide précieuse (k)(k)