Convergence d'une intégrale

[Clarissa]

Bonjour,
je n'arrive pas à montrer la convergence de l'intégrale de cos(x²) dont les bornes vont de 0 à + l'infini .

Merci de votre aide.

(aussi je suis nouvelle sur le forum et je me demandais s'il y avait possibilité d'utiliser des outils mathématiques dans le message comme ici une intégrale par exemple ou une somme, comment fait-on?) Merci

[murray]

bonjour,
en développant cos(x²) en série entière puis en inversant somme et intégrale tu obtiendras peut-être quelque chose..
une remarque quand au terme convergence: il me semble que celui-ci est inapproprié. On ne dit pas qu'une intégrale converge mais qu'elle existe.
En tout cas c'était le cas il y a 3 ans lorsque j'étais en Mathspé. Ceci dit les programmes ont du changer depuis

[mathelot]

faire le changement de variable puis vérifier le critère de Cauchy



lorsque ce critère est vérifié, votre intégrale est convergente (ou définie..)

[Chimomo]

Une intégrale existe si la fonction est intégrable ou si l'intégrale converge me semble-t-il, mais dites moi si je me trompe.

[Clarissa]

oulala c'est pas évident tout ça... je vais essayer.Merci pour vos réponses.

[fonfon]

Salut, pour les outils mathématiques:
->http://www.maths-forum.com/showthread.php?t=3414

A+

[Clarissa]

J'y arrive toujours pas, je vois pas l'astuce...pas évident.

[yos]

Après le changement de variable u=x², je suggère une IPP pour se ramener à une intégrale absolument convergente.
Pour chimomo :
intégrale existe=intégrale convergente
fonction intégrable= intégrale absolument convergente.

[tize]

autre méthode plus académique en rapport avec la methode de Mathelot:
tu poses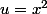 et ensuite tu as :

tu découpes ensuite l'integrale grace a des intervalles (cos est periodique) et tu majore alors ton integrale par une série semi convergente et tu fais tendre Y vers l'infini.
Enfin... si je dis pas de bêtises ...


tout a fait d'accord avec Yos aussi, je trouve ca même mieux

[Chimomo]

Je le savais Yos, mais tu confirme ce que je disais, si on dit qu'une intégrale existe ca veut dire qu'elle converge mais pas forcément qu'il s'agit de l'intégrale d'un fonction intégrable.

[sebi]

une fonction f est integrable si l'intégrale |f| est finie. si l'intégrale de |f| est infini, et l'intégrale de f est fini alors f est semi convergente

[Luc]

en fait il y a plus simple ; fais ce quon appelle une "intégration par parties forcée" pour pouvoir intégrer le sin(x^2) (comme le filtre intégrateur qui "aplatit" le signal sinusoidal en physique)

il suffit d'écrire cos(x^2)=2x/2x cos(x^2)
En coupant l'intégrale en 1 (pour ne pas avoir de pb en 0 avec le 1/x^2 qui va apparaitre), il vient

intégrale de 0 à l'infini de cos(x^2) = intégrale de 0 à 1 (qui est bornée) + intégrale de 1 à l'infini de 2x/2x cos(x^2)

Par parties, le deuxieme terme est egal au crochet de 1/2x*sin(x^2) entre 1 et l'infini (borné) + intégrale de 1 à l'infini de sin(x^2)/(2*x^2) qui converge (par exemple en disant quelle converge absolument par comparaison a l' intégrale de 1/x^2)