Bonjour,
J'ai un petit problème sur un exo traitant de convergence au sens
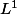
et

Soit
 = \sqrt{n} e^{-n^2 x^2})
. Le but de l'exo est d'étudier la convergence des
_{n\in \mathbb{N}})
selon les deux normes
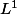
et

et de dire vers quelle fonction tend alors la suite de fonctions.
Je pense qu'il faut utiliser le théorème de convergence dominée version
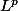
mais le résultat tombe trop vite, c'est pourquoi je pense passer à côté de l'exo.
En effet vu que les

convergent simplement vers la fonction nulle et que pour tout compact

 \leq e^{-x^2})
qui appartient à
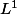
et

(selon la mesure de Lebesgue).
On a donc directement par le théorème que

tend vers la fonction nulle au sens
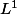
et

.
J'arrive pas à trouver l'erreur, surtout qu'en calculant je trouve
^{\frac{1}{4}})
Merci d'avance!
