Bon je déterre ce post parce que c'est là dessus qu'on tombe quand on tape "convergence faible sobolev" dans google et que j'ai pas trouvé grand chose d'autre sur le sujet. Au final je ne connais pas de caractérisation de la convergence faible dans les espaces de sobolev mais peut être que mon post sera utile à certaines personnes.
Petite remarque avant de commencer : en france la convention est de noter par un prime la dual topologique et par une étoile le dual algébrique. Chez les anglophones c'est l'inverse...
La principale difficulté vient du fait que l'on a pas de caractérisation sympathique du dual d'un espace de sobolev en général. Même quand il s'agit de
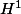
il faut faire attention car on ne peut l'identifier avec son dual (cf Brezis)
Soit

un ouvert de
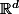
. On se passera d'écrire le

dans
)
,
)
etc... et on notera p' l'exposant conjugué de p, ainsi L^p'=(L^p)'.
Soit
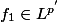
et
^d)
deux fonctions, on peut alors définir une forme linéaire continue sur
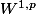
comme ceci :
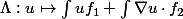
. Si

dans
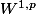
alors forcément
 \rightarrow \Lambda(u))
quelque soit les fonctions
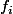
choisies. En particulier en prenant
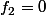
on en déduit que

dans
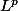
et en prenant
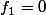
et

nulle sur toute ses composantes sauf une on en déduit

dans
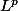
. Le sens que egan a réussi à démontrer.
Maintenant si on se place dans le cas favorable où

est un ouvert borné et régulier et que
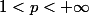
on sait que
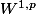
s'injecte de façon compacte dans
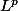
. Soit
_k)
une sous suite fortement convergente dans
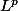
vers une limite

, puisqu'elle est aussi faiblement convergente vers

dans
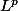
on sait que

. En utilisant un lemme de Cantor (une suite converge vers une limite x si et seulement si de toute sous suite extraite on peut extraire une sous sous suite convergente de limite x) et le fait que toute sous suite extraite de
_n)
est fortement relativement compacte on en déduit que

dans
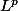
. On a donc réussi à transformer la convergence faible de départ en une convergence forte. On ne peut évidemment pas faire la même chose avec le gradient de

, sinon on aurait équivalence entre convergence forte et faible, ce qui est impossible. D'ailleurs on peut facilement montrer qu'on a pas convergence forte de la dérivée en donnant un contre exemple à base d'une fonction en dent de scie dont la dérivée alterne entre +1 et -1 et converge faiblement vers 0
Cependant même dans ce cas je ne sais pas si cela est suffisant pour montrer l'autre sens de l'implication. Le problème étant toujours qu'on ne sait pas "à quoi ressemble" le dual de
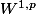
, peut être est-il bien plus grand que le simple espaces des fonctionelles
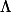
définies plus haut. Cependant ce n'est pas forcément très grave, dans les situations que j'ai pu rencontrer en pratique il n'était jamais utile de savoir comment se comporte une suite
)
"au regard" d'hypothétiques formes linéaire tarabiscotés qu'on ne pourrait pas écrire comme les
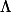
définies plus haut.
