Convergence Faible dans un Sobolev

[geo_83]

Bonsoir,

J'ai un petit trou de mémoire.

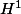
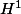
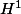
Si appartient à , converge faiblement vers et si est bornée en norme alors converge faiblement vers .

Je sais que c'est vrai mais je sais plus pourquoi exactement ?
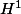
Je pense à ça : converge faiblement vers un pour une sous suite, mais pourquoi ?
Qq'un peut m'aider ?

[geo_83]

je reposte à nouveau, en espérant que quelqu'un sache répondre...

[Finrod]

ça ressemble au thm de Rellich...

[geo_83]

Salut !!
Merci pour la réponse, j'ai vu que le théorème de Rellich traite des injections de Sobolev.
Donc on déduit que la suite converge dans faible et par unicité de la limite faible, .
Cet argument suffit ?

[Finrod]

S'il te manque juste u=v à montrer, on dirait bien oui.

Je n'en sais à priori pas plus que toi sur les Sobolev. Je peux juste dire que le raisonnement est juste. Il y a peut être plus court.

[geo_83]

OK merci :happy2:

[ffpower]

En esperant ne pas m embrouiller Si u_n->v faiblement dans H^1, Ca signifie que pour tout w de H^1 (u_n,w)->(v,w). Comme H^1 est dense dans L^2, et que u_n est bornée dans L^2 ( car dans H^1) , ca implique que la convergence précédente est valide pour en fait tout w de L^2. Donc u_n tend faiblement vers v, donc v=u