Continuité de fonctions de deux variables

[Gurvan44]

Salut !
Je suis sur l’étude de fonctions de plusieurs variables assez basiques mais je galère quand même, voilà à quoi ressemblent-t-elles :

https://drive.google.com/open?id=1bUIJJ ... VWF8aaXmdg

(il y a énoncé + correction du manuel)


Il s’agit d’étudier leur continuité ainsi que celles de leur ddp (dérivées partielles premières)
Auriez vous deux trois conseils ? de vidéo sur le sujet ou exos bien corrigés quelque part ?
Car la correction de mon livre est bien succincte

(Si vous avez le courage de m’en expliquer une j’ai en particulier du mal avec la d) et la h), je pense qu’il sera plus clair et plus simple que vous m’envoyiez une photo de ce que vous avez écrit plutôt que de taper ça sur le chat !)

Merci d’avance !

[Ben314]

Salut,
La méthode "de base" pour montrer qu'une fonction f de deux variables tend vers L lorsque (x,y) tend vers (xo,yo), c'est :
- Au cas où (xo,yo) n'est pas égal à (0,0), commencer par "poser" x=xo+h, y=yo+k avec (h,k) qui tend vers (0,0) [quasiment toutes les limites connues "par coeur" sont en 0]
- Ensuite, tu essaye de majorer |f(x,y)-L| par un truc qui ne dépend que de la norme N de (x,y) [ou de (h,k) si tu as fait un changement de variable] sachant que, pour la norme, tu peut prendre soit la norme1, soit la norme2, soit la norme infini : ça dépend de la tête de ta fonction (avec quoi ça sera le plus facile de majorer).
Le but étant bien sûr de majorer par quelque chose qui tend vers 0 lorsque N tend vers 0.

Tout ça, c'est au cas où effectivement la limite existe. Par contre, pour montrer que la limite n'existe pas, il suffit de trouver deux "cas particuliers" (par exemple x=0 et y->0 ou bien x->0 et y=0 ou bien y=x avec x->0) qui ne donnent pas la même limite.

[Ben314]

Sinon, on peut regarder par exemple la d) où .

Le programme, normalement, c'est :

1) Est-elle "bien définie" sur R^2 ? et où est elle "trivialement" continue ?
2) En l'endroit (ou les endroits) qui pose problème, est-elle continue ?
3) Où est-ce qu'elle admet "trivialement" des dérivées partielles continues ?
4) En l'endroit (ou les endroits) où l'existence de dérivées partielles n'est pas évidente, les dérivées partielles existent-elles ?
5) Si oui, y-a-t-il continuité des dérivées partielles en ces points là ?

Qu'à tu fait pour le moment ?

[Gurvan44]

Merci bcp de ta réponse, ouai la méthode que tu me décris correspond bien à ce qui est dit dans mon livre
je viens d'ajouter ma réponse en photo sur le dossier drive que j'ai linké en 1er msg.

[Ben314]

---

[Ben314]

Pour le b)

- Au départ, tu peut effectivement affirmer "gratos" que la fonction est continue partout (composée de fonction continue) mais aussi qu'elle admet des dérivées partielles partout sauf éventuellement lorsque vu que c'est une composée de fonction dérivables sauf la fonction valeur absolue qui n'est pas dérivable en 0.

- Ensuite, en regardant de plus près, les dérivées partielles en x existent absolument partout vu que, pour y fixé, la fonction est évidement partout dérivable. Et on a (absolument partout) qui est évidement continue (composée de fonction continues).

- Pour , c'est très différent (mais pas bien compliqué) : si on considère x comme fixé alors la fonction sera évidement dérivable pour tout 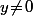, mais par contre, elle ne sera jamais dérivable en (sauf si le coefficient constant est nul) vu que n'est pas dérivable en 0.
Le bilan, c'est que n'existe que pour les tels que 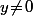ainsi que pour :
.
Concernant la continuité de , je sais pas si c'est bien intéressant à étudier vu le domaine de définition "un peu bizarre" mais on peut quand même regarder :
- En tout tel que la fonction est continue car égale soit à soit à (toute les deux continues) pour tout les suffisamment proche de .
- En tout avec la question ne se pose pas vu que de toute façon la fonction n'est pas définie en un tel point.
- En la fonction est continue vu que, lorsque existe, on a ce qui prouve que .

[Gurvan44]

ok ok merci beaucoup, juste aurais tu développé le numérateur du d) ? pour le majorer ? ou il y a un moyen plus efficace ? car dans la correction il semblerait qu'il y ait plus rapide en utilisant le max(x,y) mais je ne vois pas bien comment m'en sortir avec ça..

[Ben314]

Non, j'aurais fait comme toi : la minoration elle "saute aux yeux" et, vu le numérateur, elle est suffisante pour avoir une majoration de |f(x,y)| qui permet de conclure.
Donc pourquoi s’embêter à chercher plus compliqué. Et je ne vois pas comment tu pourrait faire "plus rapide" vu que ta façon de procéder ne contient aucun calcul à part triviaux (style x^5/x^4=x)
Et par contre, de majorer le dénominateur, vu le contexte, ça ne sert à rien vu que ça permettrais de minorer la fonction ce qui est inutile.

[Gurvan44]

ok ca marche, dernière question (j'adore tes réponses alors je profite ^^) pour la i) et j), je vois bien pour la i) que f'x(x,y) n'est pas défini dans l'ensemble B1 (cf "correction i et j" sur le lien), d'aillleurs, on est d'accord qu'elle est bien non définie ? ce n'est pas seulement non continue ? genre c'est bien le "même" cas que valeur absolue dans R ?
Mais pour la j) je ne vois pas du tout pq elle serait définie en (0,0)...

[Ben314]

Que ce soit pour la i) et la j), tu peut (voire même tu doit) commencer par dire que, vu que toute les fonction intervenant dans la définition de f sont continues et dérivable partout SAUF la valeur absolue qui n'est pas dérivable en 0 (mais qui est continue), ça prouve que f est continue partout et dérivable (en x et en y) partout sauf éventuellement lorsque ce qu'il y a dans la valeur absolue est nul.

Par contre, il faut faire gaffe au fait que le th. de dérivation d'une composée, ce qu'il dit, c'est que, si f et g sont dérivable alors la composée est dérivable (pris en des points cohérents). Mais par contre, si par exemple g n'est pas dérivable, ça ne prouve pas que la composée ne l'est pas.
Exemple : x->|x^2| où la fonction valeur absolue n'est pas dérivable en 0 donc le théorème de composition ne permet pas de savoir si cette fonction est ou n'est pas dérivable lorsque x^2=0 (c'est à dire lorsque x=0).
Sauf qu'en fait elle l'est évidement vu que |x^2|=x^2 !!!

Bref, arrivé à ce point, il faut regarder "à la main" (c'est à dire avec des limites) si les fonctions en question sont dérivable ou pas (en x et en y) sur les points tels que ce qu'il y a dans la valeur absolue est nul.
Pour la i), tu trouve que ça ne marche jamais donc qu'elle n'est dérivable QUE si ce qu'il y a dans la valeur absolue est non nul. par contre pour la j), tu trouve que ça ne marche jamais, sauf au point (0,0).

Et si tu veut une raison "avec un peu de recul" (i.e. sans trop de calcul, mais à détailler), ça provient du fait qu'une fonction du style g:x->|f(x)|, si tu te place en un point xo où f s'annule et change de signe, les dérivées à droite et à gauche de g en xo vont être +f'(xo) et -f'(xo) qui sont différentes (donc g ne va pas être dérivable) SAUF si f'(xo)=0 (et dans ce cas là, g est effectivement dérivable en xo avec une dérivée nulle).
Par exemple, vérifie que x->|x^3|, est effectivement dérivable en 0 bien que x->x^3 change de signe en 0 (et trace le graphe de x->x^3 et de x->|x^3| pour mieux comprendre d'où ça provient)

[Gurvan44]

wow je viens de faire le x^3 en effet, je suis surpris de découvrir cela si tard ! merci beacoup je pense que c'est carrément fondamental de savoir ça fin bref je suis content ^^
ducoup je pense avoir réussi à expliquer la dérivée de j) en (0,0) mais je commence à tout remettre en question quant au cas x^2 = y^2. J'ai mis une photo sur "réponse à ben". je suis un peu perplexe
merci encore pour ton temps <3

[Ben314]

Ça me semble à peu prés O.K. au moins jusqu'au "J'ai envie de dire..." où ça devient pas clair du tout ton truc.
J'ai l'impression que tu cherche à voir si existe (donc en un point tel que ). Sauf qu’après, je comprend pas trop ce que tu écrit.
Normalement, tu devrait écrire soit , soit (c'est bien évidement exactement la même chose, mais perso, je trouve la deuxième forme plus pratique).


Ce qui signifie que la limite lorsque n'existe que lorsque , c'est à dire lorsque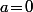

Remarque : Ce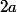 qu'on trouve, c'est bien la dérivée de en ce qui correspond à ce que je te disait dans la remarque précédente avec g=|f| et g'(xo)=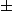f'(xo) à droite / à gauche.

[Gurvan44]

Oh oui désolé j'aurais pu me relire un minimum avec mon f(x-a,a)... ok oui très bien très clair.

Donc on peut dire assez gratuitement :
"En posant g=|f|, on a bien g'(xo)=+/-f'(xo), il suffit donc de vérifier que +f'(xo) = -f'(xo) (dérivées égales à gauche et à droite) pour étudier la continuité de f' " en adaptant évidemment les notations suivant le contexte (ici, des fonctions à deux arguments mais qu'une seule variable quand on s'intéresse à f'x(a,a))


Et finalement, il est donc inutile si j'ai bien compris de dissocier les cas x=y et x=-y (correspondant à x^2=y^2) ?

[Ben314]

Oui, c'est ça, modulo de bien faire gaffe à ce qu'on écrit dans le cas où on utilise directement g=|f| : Si f s’annule mais ne change pas de signe alors la non dérivabilité de la valeur absolue ne joue plus aucun rôle. Et si f change de signe, il faut aussi faire gaffe pour savoir de quel coté (à droite ou à gauche) qu'on va avoir g'=+f'.

Et effectivement, c'est pas forcément bien utile de différentier les cas y=x et y=-x qui sont "plus que similaire" en raisonnant en terme de g=|f|.
Après, fait gaffe quand même que tout ça, c'est assez spécifique au cas de la fonction valeur absolue donc pas super utile sur le plan théorique. Ça marche "à peu prés pareil" pour toute fonction non dérivable en un point mais qui admet des dérivées à droite et à gauche, mais on peut pas dire que ce soit un cas "super fréquent" quand on a des dérivées partielles à calculer.
Bref, c'est plutôt une "petite astuce" qu'un truc "vraiment général" : c'est pas sûr que tu t'en resserve souvent...

[Gurvan44]

oui oui j'entend bien que c'est très spécifique en tout cas merci bien à la prochaine, c'était un plaisir !