Connaître le nombre de faces d'un polyèdre quelconque

[ClubGalilee]

Bonjour à tous !

Je cherche à modéliser des objets en 3d sur OpenGl et je me retrouve face à un problème.

Peut-on savoir le nombre de faces d'un Polyèdre (fermé) composé uniquement de triangles à partir du nombre de points qui le compose ? Ou inversement (nombre de faces --> nombre de points) ?

Je ne trouve la réponse nulle part en ligne... Merci d'avance pour votre aide

[Ben314]

Salut,
Si ton polyèdre est convexe (*) alors tu peut utiliser la formule dite d'Euler qui dit que :
nombre(Faces) - nombre(arrête) + nombre(sommet) = 2.
Si tu connaît le nombre de sommet et que tu cherche le nombre de faces , vu que tes faces sont toutes des triangles, alors chaque face est bordée par 3 arrêtes ce qui fait arrêtes, sauf que tu les as compté 2 fois vu que la même arrête est commune à deux faces. Donc le vrai nombre d’arêtes de ton polyèdre est (ce qui signifie en particulier que est forcément pair).
La formule d'Euler te dit alors que c'est à dire que .

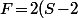(*) Ou plus généralement, s'il a le même type d'homotopie qu'une boule, c'est à dire s'il n'y a pas de "trou" dedans. Si ton polyèdre a des "trous", le =2 final est à remplacer par 2-2N où N est le nombre de "trous", mais c'est pas complètement trivial d'expliquer comment on compte le nombre de "trou" dans le cas général.

Par exemple là, tu dirait qu'il y en a combien des "trous" ? (ils traversent entièrement le cube)

[ClubGalilee]

Il y a six trous, tous entourés de quatre faces, soit 30 faces en tout pour cette forme. Merci beaucoup de ton aide, ça m'a aidé à trouvé une solution simple à mon problème! je fais de l'art, les maths c'est pas mon fort, sans ton aide j'aurais surement ramé longtemps !

[Ben314]

Non, justement, il faut faire gaffe concernant la façon de compter si tu utilise la formule d'Euler sous la forme
nombre(Faces) - nombre(Aarrête) + nombre(Sommet) = 2 - nombre(Trou)
Alors dans le cas du cube çi dessus, des "trou" il n'y en a que 5 :
- Tu part du cube (pas de trou)
- Tu perce une première fois de part en part -> un (seul) trou.
- Tu perce sur une autre face jusqu'au milieu -> un deuxième trou ; puis tu fini de percer jusqu'au fond -> un troisième trou.
- Idem sur les deux dernières face ce qui rajoute 2 trous de plus, soit 5 au total.

Une autre façon de voir le bidule, c'est de supposer le cube "tout mou" (en pâte à modeler) : tu passe les doigts dans un des trous et tu écarte pour (beaucoup) l'agrandir plus tu aplanie plus ou moins le truc pour avoir une "galette" plus ou moins plate de pâte à modeler avec des trous dedans : là tu constate bien qu'il n'y a que 5 trous et pas 6.