Probabilités de lancer de dés à 40 faces
28 messages
- Page 1 sur 2 - 1, 2
Probabilités de lancer de dés à 40 faces
Bonjour à tous,
J'ai une question de probabilité que je n'arrive pas à résoudre (mon bagage mathématique n'est pas assez important).
J'aimerais connaître le nombre de lancers que je dois faire avec un dé à 40 faces (bien équilibré) pour que la probabilité (lorsque je vais effectuer le nombre de lancers calculé) d'obtenir au moins une fois toutes les valeurs (de 1 à 40) soit de 95%.
C'est assez facile avec une pièce pour savoir le nombre de lancers que je dois faire pour avoir (au moins) 95% de chances d'obtenir au moins une fois pile et au moins une fois face.
1er lancer : peu importe
2ème : 50%
3ème : 75%
4ème : 87,5%
5ème : 93,75%
6ème : 96,875%
Donc si je veux une probabilité supérieure ou égale à 95% d'obtenir les deux valeurs possibles pour une pièce, je dois effectuer 6 lancers.
Mais dès qu'on augmente le nombre de valeurs possibles ça se complique.
Je sèche complètement (et je ne peux le faire "à la main") pour faire la même chose pour un dé à 40 faces.
Quelqu'un pourrait-t-il m'aider (me donner la réponse) ? Attention, mon niveau en math est pas fabuleux, les matrices, tout ça, c'est hyper loin ^^'
Merci d'avance
Calenloth
J'ai une question de probabilité que je n'arrive pas à résoudre (mon bagage mathématique n'est pas assez important).
J'aimerais connaître le nombre de lancers que je dois faire avec un dé à 40 faces (bien équilibré) pour que la probabilité (lorsque je vais effectuer le nombre de lancers calculé) d'obtenir au moins une fois toutes les valeurs (de 1 à 40) soit de 95%.
C'est assez facile avec une pièce pour savoir le nombre de lancers que je dois faire pour avoir (au moins) 95% de chances d'obtenir au moins une fois pile et au moins une fois face.
1er lancer : peu importe
2ème : 50%
3ème : 75%
4ème : 87,5%
5ème : 93,75%
6ème : 96,875%
Donc si je veux une probabilité supérieure ou égale à 95% d'obtenir les deux valeurs possibles pour une pièce, je dois effectuer 6 lancers.
Mais dès qu'on augmente le nombre de valeurs possibles ça se complique.
Je sèche complètement (et je ne peux le faire "à la main") pour faire la même chose pour un dé à 40 faces.
Quelqu'un pourrait-t-il m'aider (me donner la réponse) ? Attention, mon niveau en math est pas fabuleux, les matrices, tout ça, c'est hyper loin ^^'
Merci d'avance
Calenloth
Re: Probabilités de lancer de dés à 40 faces
Tu demandes en fait un calcul d'espérance: en combien de coups en moyenne obtiendrais je "n" faces différentes ?
Je n'ai pas fait ça souvent, mais il me semble que c'est 40 (1/40 + 1/39 + 1/38 + ....1/1) = 171 environ.
A confirmer !
Je n'ai pas fait ça souvent, mais il me semble que c'est 40 (1/40 + 1/39 + 1/38 + ....1/1) = 171 environ.
A confirmer !
Re: Probabilités de lancer de dés à 40 faces
Oui absolument nodgim, ce problème est connu sous le nom de "coupon collector's problem", ou "problème du collectionneur de vignettes" en français.
En moyenne, il te faudra , où
, où est le 40ème nombre harmonique, soit environ
est le 40ème nombre harmonique, soit environ +\gamma)+\frac{1}{2}) lancers, soit environ 171 lancers.
lancers, soit environ 171 lancers.
Cependant, il peut avoir des déviations par rapport à cette espérance, je suis en train de rechercher un intervalle de confiance à 95%.
En moyenne, il te faudra
Cependant, il peut avoir des déviations par rapport à cette espérance, je suis en train de rechercher un intervalle de confiance à 95%.
Modifié en dernier par LB2 le 27 Juin 2018, 11:34, modifié 3 fois.
Re: Probabilités de lancer de dés à 40 faces
………………………...
Modifié en dernier par beagle le 27 Juin 2018, 14:06, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités de lancer de dés à 40 faces
……………………...
Modifié en dernier par beagle le 27 Juin 2018, 14:06, modifié 2 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités de lancer de dés à 40 faces
………………
beaucoup trop cher, invendable
beaucoup trop cher, invendable
Modifié en dernier par beagle le 27 Juin 2018, 14:07, modifié 2 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités de lancer de dés à 40 faces
LB2 a écrit:Cependant, il peut avoir des déviations par rapport à cette espérance, je suis en train de rechercher un intervalle de confiance à 95%.
Une valeur
Avec
D'où cette valeur
En faisant 184 lancers du dé équilibré à 40 faces, tu as 95% de chances d'obtenir au moins une fois toutes les faces.
Re: Probabilités de lancer de dés à 40 faces
Ah OK, il avait demandé en effet un calcul de proba, pas d'espérance.
Re: Probabilités de lancer de dés à 40 faces
nodgim a écrit:Ah OK, il avait demandé en effet un calcul de proba, pas d'espérance.
les deux étant liés via le théorème central limite
Re: Probabilités de lancer de dés à 40 faces
LB2 a écrit:nodgim a écrit:Ah OK, il avait demandé en effet un calcul de proba, pas d'espérance.
les deux étant liés via le théorème central limite
Je connais bien les ailiers, mais pas trop les attaquants d'axe, si tu dis qu'ils sont limités.....
Re: Probabilités de lancer de dés à 40 faces
Salut,
C'est pas parce que, tels les no brain, une grande partie des statisticiens font comme si tout était régi par la loi normale qu'il faut en faire autant !!!
Perso, et avec un bête tableur, je trouve que :
Après 263 lancers, la proba d'avoir obtenu chacune des les 40 faces au moins une fois est de 94,975 %
Après 264 lancers, la proba d'avoir obtenu chacune des les 40 faces au moins une fois est de 95,098 %
Je comprend pas d'où tu sort ta loi normale vu le problème posé...LB2 a écrit:Une valeurest telle que la probabilité d'obtenir toutes les faces du dé à n faces au moins une fois en moins de
lancers est de 95%.
Avecnombre de faces
la valeur du quantile à 5% de la loi normale centrée réduite
l'écart-type du nombre de lancers nécessaire
D'où cette valeurlancers!
En faisant 184 lancers du dé équilibré à 40 faces, tu as 95% de chances d'obtenir au moins une fois toutes les faces.
C'est pas parce que, tels les no brain, une grande partie des statisticiens font comme si tout était régi par la loi normale qu'il faut en faire autant !!!
Perso, et avec un bête tableur, je trouve que :
Après 263 lancers, la proba d'avoir obtenu chacune des les 40 faces au moins une fois est de 94,975 %
Après 264 lancers, la proba d'avoir obtenu chacune des les 40 faces au moins une fois est de 95,098 %
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Probabilités de lancer de dés à 40 faces
Bon alors attention après ma belle intervention d'hier matin où le nombre de doublons devaient juste se compter en milliard!!!!
Another one qui n'est pas le calcul exact, mais on peut voir ce que l'on pert en approximant ainsi:
1 - 40x(39/40)^263 = 0,948
1- 40x(39:40)^264= 0,94996
Mais bon je suis assez champion à trouver des justifications à postériori, sachant que!
Comme les réseaux de neurones d'ailleurs, non?
Another one qui n'est pas le calcul exact, mais on peut voir ce que l'on pert en approximant ainsi:
1 - 40x(39/40)^263 = 0,948
1- 40x(39:40)^264= 0,94996
Mais bon je suis assez champion à trouver des justifications à postériori, sachant que!
Comme les réseaux de neurones d'ailleurs, non?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités de lancer de dés à 40 faces
Bonjour
je pose z=40, puisque 40 faces.
La proba d'avoir obtenu chacune des 40 faces au moins une fois exactement au n-ième lancer et pas avant, est :
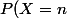 =)
 ^{z-i+1}{z-1\choose i} \left( {<br />\frac {i}{z}} \right) ^{n-1})
pour
exactement comme Ben314 l'a annoncé :
Après 263 lancers, la proba d'avoir obtenu chacune des 40 faces au moins une fois est de P(40)+...+P(263) = 0.94975
Après 264 lancers, la proba d'avoir obtenu chacune des 40 faces au moins une fois est de P(40)+...+P(264) = 0.95098
je pose z=40, puisque 40 faces.
La proba d'avoir obtenu chacune des 40 faces au moins une fois exactement au n-ième lancer et pas avant, est :
pour
exactement comme Ben314 l'a annoncé :
Après 263 lancers, la proba d'avoir obtenu chacune des 40 faces au moins une fois est de P(40)+...+P(263) = 0.94975
Après 264 lancers, la proba d'avoir obtenu chacune des 40 faces au moins une fois est de P(40)+...+P(264) = 0.95098
Re: Probabilités de lancer de dés à 40 faces
Pareil résultat: Beagle n'est pas loin, Leon a fait le calcul juste.
Le fait est que, dans le calcul exact de la proba, plus la puissance est élevée ( ici 263 ) et plus le seul 1er terme est proche du résultat. Le 2ème terme : 40*39/2 * (38/40) ^263 est déjà nettement plus petit que le premier.
Le fait est que, dans le calcul exact de la proba, plus la puissance est élevée ( ici 263 ) et plus le seul 1er terme est proche du résultat. Le 2ème terme : 40*39/2 * (38/40) ^263 est déjà nettement plus petit que le premier.
Re: Probabilités de lancer de dés à 40 faces
nodgim a écrit:Pareil résultat: Beagle n'est pas loin, Leon a fait le calcul juste.
Le fait est que, dans le calcul exact de la proba, plus la puissance est élevée ( ici 263 ) et plus le seul 1er terme est proche du résultat. Le 2ème terme : 40*39/2 * (38/40) ^263 est déjà nettement plus petit que le premier.
Pas d'internet ce WE, je réponds maintenant.
Tout a fait d'accord avec la remarque de nodgim, tout est dit rapidement avec ^263
avec un seul terme de pris ma soustraction était "trop forte" de très peu
avec deux termes la soustraction devient un peu trop faible, mais on est déjà avec une grosse précision
1 -[40x(39/40)^263 - C(40,2)x(38/40)^263)] = 0,949761
contre 0,94975 de Ben314
et
idem en ^264
donne 0,950990
contre 0,95098 de Ben 314
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités de lancer de dés à 40 faces
Et donc, l'utilisation du "Problème du collectionneur de vignettes" n'est pas envisageable ici ?
Car la différence de valeur est vraiment importante suivant le calcul (171 et 263)
Car la différence de valeur est vraiment importante suivant le calcul (171 et 263)
Re: Probabilités de lancer de dés à 40 faces
calenloth a écrit:Et donc, l'utilisation du "Problème du collectionneur de vignettes" n'est pas envisageable ici ?
Car la différence de valeur est vraiment importante suivant le calcul (171 et 263)
et bien si tu peux,
40logn(40) =147 il faut rajouter 23 avec la constante d'Euler -...
c'est cela votre 171?
mais ça on dirait que c'est la moyenne
alors l'écart-type lui il est à 50, 40pi/squareroot6 fait 51.3
bon alors pour avoir du 95%, il faut un peu moins de deux écart-types si on se ramène à Gauss unilatéral pour les 5%
donc on va pas arriver à 263? Sur?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités de lancer de dés à 40 faces
Le 171 est l'espérance, c'est à dire qu'en moyenne il faut lancer le dé 171 fois pour avoir les 40 faces.
Re: Probabilités de lancer de dés à 40 faces
Il semblerait que LB2 avait tout pour le faire selon le "problème du collectionneur de vignette"
cad espérance à 171 et écart type à 50
perso j'ai 51,3 pour 40pi/racine carrée6
si on prend comme le disait LB2 et comme on l'avait révisé grace à Pascal
superieur/inf-chaque-cote-t195297.html
si on prend 5% unilatéral sur la courbe de Gauss avec écart-type qui tombe à 1,644 (contre 1,96 pour 5ù bilateral)
bref j'ai alors 84,3 après moyenne
donc 171 +84 = 255
255 c'est déjà plus proche de la valeur théorique de 264,
mais c'est pas terrible quand même,
et à mon avis cela signifie juste que approximer les lois binomiales, polynomiales, autres avec la loi normale,
ben cela marche d'autant mieux que les nombres sont élevés.
Alors avec les puissances de 263 et 264 on a vu grace à la remarque de nodgim que tout est joué rapidement,
pour autant c'est le 40 qui est trop faible pour avoir une super bonne approximation par la loi normale.
Si j'ai le temps j'essaierai un n bien sup à 40.
Ou si un membre du forum veut faire un n consequent pour voir que l'approximation par la loi normale va se justifier...
cad espérance à 171 et écart type à 50
perso j'ai 51,3 pour 40pi/racine carrée6
si on prend comme le disait LB2 et comme on l'avait révisé grace à Pascal
superieur/inf-chaque-cote-t195297.html
si on prend 5% unilatéral sur la courbe de Gauss avec écart-type qui tombe à 1,644 (contre 1,96 pour 5ù bilateral)
bref j'ai alors 84,3 après moyenne
donc 171 +84 = 255
255 c'est déjà plus proche de la valeur théorique de 264,
mais c'est pas terrible quand même,
et à mon avis cela signifie juste que approximer les lois binomiales, polynomiales, autres avec la loi normale,
ben cela marche d'autant mieux que les nombres sont élevés.
Alors avec les puissances de 263 et 264 on a vu grace à la remarque de nodgim que tout est joué rapidement,
pour autant c'est le 40 qui est trop faible pour avoir une super bonne approximation par la loi normale.
Si j'ai le temps j'essaierai un n bien sup à 40.
Ou si un membre du forum veut faire un n consequent pour voir que l'approximation par la loi normale va se justifier...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Probabilités de lancer de dés à 40 faces
Ce n'est pas tant le 40 qui est trop faible, mais c'est plutôt le 95% qui génère l'écart. Plus précisément, 1-0.95 = 0.05. En fait, on peut grosso modo dire que le résultat avec le seul 1er terme 40 * (39/40 ) ^ n possède une précision de l'ordre du pourcentage réclamé. Pour 95 % demandé, le "n" correspondant donne au 1er terme une précision à moins de 5 %, et ça se montre facilement. Si on avait demandé 99 %, on aurait eu un résultat bon à moins de 1 % près.
28 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
